Basit Işıklandırma

Gerçek dünyadaki ışıklandırma son derece karmaşıktır ve çok fazla faktöre bağlıdır, bu da sahip olduğumuz sınırlı işlem gücüyle hesaplayamayacağımız bir şeydir. Bu nedenle OpenGL' de ışıklandırma, işlenmesi çok daha kolay olan ve nispeten benzer görünen basitleştirilmiş modeller kullanan gerçeklik yaklaşımlarına dayanmaktadır. Bu ışıklandırma modelleri, anlayabileceğimiz gibi ışığın fiziğine dayanmaktadır. Bu modellerden birine $\green{Phong\ aydınlatma\ modeli}$ denir. Phong aydınlatma modeli 3 bileşenden oluşur: ortam (ing. ambient), dağınık (ing. diffuse) ve düzgün (ing. specular) ışıklandırma. Aşağıda bu ışıklandırma bileşenlerinin kendi başlarına ve karma olarak nasıl göründüklerini görebilirsiniz:

• $\green{Ortam\ Işıklandırması}$ : Karanlık olduğunda bile, dünyanın bir yerinde (ay, uzak bir ışık) genellikle halen bir miktar bulunur, bu yüzden nesneler neredeyse hiçbir zaman tamamen karanlık değildir. Bunu benzetimlemek için, nesneye her zaman biraz renk veren bir ortam aydınlatma sabiti kullanıyoruz.

• $\green{Dağınık\ Işıklandırma}$ : Bir ışık nesnesinin bir nesne üzerindeki yönlü etkisini benzetimler. Bu, ışıklandırma modelinin görsel olarak en önemli bileşenidir. Bir nesnenin bir kısmı ışık kaynağına ne kadar çok bakarsa o kadar parlak olur.

• $\green {Düzgün\ Işıklandırma}$ : Parlak nesnelerde görünen ışığın, parlak noktasını benzetimler. Düzgün vurgular ışığın rengine, nesnenin renginden daha yatkındır.

Görsel olarak ilginç sahneler oluşturmak için en azından bu 3 ışıklandırma bileşenini benzetimlemek istiyoruz. En basit olanla başlayacağız: ortam ışıklandırması.

Ortam Işıklandırması

Işık genellikle tek bir ışık kaynağından gelmez, ancak anında görünür olmadıklarında bile, etrafımıza dağılmış birçok ışık kaynağından oluşmaktadır. Işığın özelliklerinden biri, doğrudan görünmeyen noktalara ulaşarak birçok yöne dağılabilmesi ve sıçrayabilmesidir; böylece ışık diğer yüzeylere yansıyabilir ve bir nesnenin ışıklandırılması üzerinde dolaylı bir etkiye sahip olabilir. Bunu dikkate alan algoritmalara $\green{global\ aydınlanma\ (ing. global\ illumination)}$ algoritmaları denir, ancak bunların hesaplanması karmaşık ve maliyetlidir.

Karmaşık ve pahalı algoritmaların hayranları olmadığımızdan, çok basit bir küresel aydınlatma modeli, yani $\green{ortam\ ışıklandırması}$ kullanarak başlayacağız. Önceki bölümde gördüğünüz gibi, nesnenin parçalarının nihai sonuç rengine eklediğimiz küçük bir sabit (ışık) rengi kullanıyoruz, böylece doğrudan bir ışık kaynağı olmasa bile her zaman etrafa saçılan bir ışık varmış gibi görünmesini sağlıyoruz. .

Sahneye ortam ışıklandırması eklemek gerçekten çok kolaydır. Işığın rengini alıyoruz, küçük sabit bir ortam faktörü ile çarpıyoruz, bunu da nesnenin rengiyle çarpıyoruz ve küp nesnesinin gölgelendiricisinde parçanın rengi olarak kullanıyoruz:

void main()
{
    float ambientStrength = 0.1;
    vec3 ambient = ambientStrength * lightColor;

    vec3 result = ambient * objectColor;
    FragColor = vec4(result, 1.0);
}  

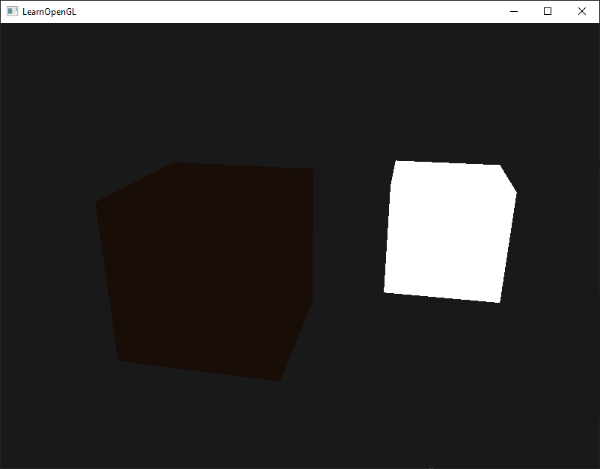
Şimdi programı çalıştırdığınızda, ışıklandırmanın ilk aşamasının nesneye başarıyla uygulandığını göreceksiniz. Nesne oldukça karanlık, ancak ortam aydınlatması uygulandığından tamamen karanlık değildir (farklı bir gölgelendirici kullandığımız için ışık küpünün etkilenmediğine dikkat edin). Aşağıdaki görseldeki gibi bir şeye benzemeli:

Dağınık ışıklandırma

Ortam ışıklandırması tek başına en ilginç sonuçları üretemez, ancak dağınık ışıklandırma nesne üzerinde önemli bir görsel etki vermeye başlayacaktır. Dağınık ışıklandırma, nesneye, parçaları bir ışık kaynağından gelen ışık ışınlarına ne kadar yakınsa, daha fazla parlaklık verir. Dağınık ışıklandırmayı daha iyi anlamak için aşağıdaki görsele bir göz atın:

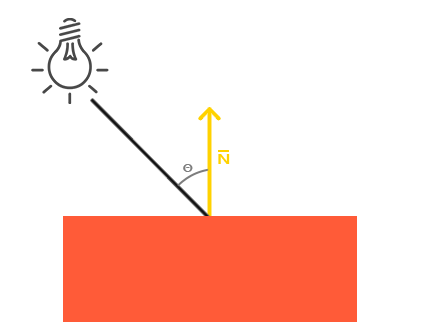
Solda, nesnemizin tek bir parçasını hedef alan bir ışık ışını olan bir ışık kaynağı görüyoruz. Işık ışınının parçaya hangi açıda dokunduğunu ölçmemiz gerekir. Işık ışını nesnenin yüzeyine dikse, ışık en büyük etkiyi yaratacaktır. Işık ışını ve parça arasındaki açıyı ölçmek için, $\green{normal\ vektör}$ adı verilen bir şeyi kullanırız, yani parçanın yüzeyine dik bir vektör (burada sarı bir ok olarak gösteriliyor) ki bunu daha sonra ele alacağız. İki vektör arasındaki açı ise iç çarpım ile kolayca hesaplanabilir.

Dönüşümler bölümünden, iki birim vektör arasındaki açı ne kadar düşük olursa, iç çarpımın 1 değerine o kadar meyilli olduğunu hatırlayabilirsiniz. Her iki vektör arasındaki açı 90 derece olduğunda, iç çarpım 0 olur. Aynısı θ için de geçerlidir: θ büyüdükçe, ışığın parçanın rengi üzerindeki etkisi azalır.

Her iki vektör arasındaki açının (sadece) kosinüsünü elde etmek için birim vektörlerle (uzunluğu 1 birim olan vektörler) çalışacağımızı unutmayın, bu nedenle tüm vektörlerin normalleştirildiğinden emin olmamız gerekir, aksi takdirde iç çarpım kosinüsten daha fazla olarak geri döner (bkz. Dönüşümler).

Sonuçta elde edilen iç çarpım, ışığın parçanın rengi üzerindeki etkisini hesaplamak için kullanabileceğimiz bir skaler değer döndürerek ışığa doğru yönlerine göre farklı ışıklandırılmış parçalara neden olur.

Peki, dağınık ışıklandırmayı hesaplamak için neye ihtiyacımız var:

• Normal vektörü: köşe noktasının yüzeyine dik olan bir vektör.

• Yönlendirilmiş ışık ışını: Işığın konumu ile parçanın konumu arasındaki fark vektörü olan bir yön vektörüdür. Bu ışık ışınını hesaplamak için ışığın konum vektörüne ve parçanın konum vektörüne ihtiyacımız vardır.

Normal vektörleri

Bir normal vektörü, bir köşe noktasının yüzeyine dik olan bir (birim) vektördür. Bir köşe noktası kendi başına yüzeye sahip olmadığından (uzayda sadece tek bir nokta olduğundan), köşe noktasının yüzeyini bulmak için çevresindeki köşeleri kullanarak normal bir vektör elde ederiz. Çapraz çarpım kullanarak küpün tüm köşeleri için normal vektörleri hesaplamak için küçük bir hile kullanabiliriz, ancak 3- boyutlu küp karmaşık bir şekil olmadığından bunları köşe verilerine el ile ekleyebiliriz. Güncellenmiş köşe noktası veri dizisini burada bulabilirsiniz. Normallerin aslında her bir düzlemin yüzeyine dik vektörler olduğunu hayal etmeye çalışın (bir küp 6 düzlemden oluşur).

Vertex dizisine fazladan veri eklediğimiz için küpün vertex shader'ını güncellememiz gerekir:

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
...

Artık köşelerin her birine normal bir vektör eklediğimize ve vertex shader'ı güncellediğimize göre, vertex attribute pointer'ları da güncellemeliyiz. Işık kaynağının küpünün, köşe verileri için aynı vertex dizisini kullandığını, ancak abajurun yeni eklenen normal vektörleri kullanmadığını unutmayın. Lambanın tonlandırıcılarını veya öznitelik konfigürasyonlarını güncellememiz gerekmiyor, ancak en azından vertex attribure pointer'larını yeni vertex dizisinin boyutunu yansıtacak şekilde değiştirmemiz gerekiyor:

glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(float), (void*)0);
glEnableVertexAttribArray(0);

Her köşenin yalnızca ilk 3 float değerini kullanmak ve son 3 float değerini yok saymak istiyoruz, bu nedenle stride parametresini bir float'ın 6 katı büyüklüğünde güncellememiz gerekiyor ve işimiz bitiyor.

Lamba tonlandırıcı tarafından tamamen kullanılmayan vertex verilerinin kullanılması verimsiz görünebilir, ancak vertex verileri konteyner nesnesinden GPU'nun belleğinde zaten depolanmıştır, bu nedenle GPU'nun belleğine yeni veriler depolamamız gerekmez. Bu aslında, lamba için özel olarak yeni bir VBO tahsis etmeye kıyasla daha verimli hale getirir.

Tüm ışıklandırma hesaplamaları fragment shader üzerinde yapılır, bu nedenle normal vektörleri vertex shader'dan fragment shader'a iletmemiz gerekir. Hadi bunu yapalım:

out vec3 Normal;

void main()
{
    gl_Position = projection * view * model * vec4(aPos, 1.0);
    Normal = aNormal;
} 

Yapılması gereken, fragment shader üzerinde karşılık gelen girdi değişkenini bildirmektir:

in vec3 Normal;  

Dağınık (ing. Diffuse) rengin hesaplanması

Artık her bir vertex için normal vektörümüz var, ancak yine de ışığın konum vektörüne ve parçanın konum vektörüne ihtiyacımız var. Işığın konumu tek bir statik değişken olduğundan, onu fragment shader'da uniform olarak bildirebiliriz:

uniform vec3 lightPos;  

Ardından, sahneleme döngüsündeki uniform değişkeni güncelleyin (veya çerçeve başına değişmediği için out). Dağınık ışık kaynağının konumu olarak önceki bölümde açıklanan lightPos vektörünü kullanıyoruz:

lightingShader.setVec3("lightPos", lightPos);  

O zaman ihtiyacımız olan son şey gerçek parçanın konumudur. Dünya uzayındaki tüm ışıklandırma hesaplamalarını yapacağız, bu yüzden önce dünya uzayında olan bir vertex konumu istiyoruz. Bunu, onu dünya-uzay koordinatlarına dönüştürmek için vertex konumu özniteliğini yalnızca model matrisiyle (görünüm ve izdüşüm matrisiyle değil) çarparak başarabiliriz. Bu, vertex shader'da kolayca gerçekleştirilebilir, bu nedenle outtipinde bir değişken tanımlayalım ve dünya-uzay koordinatlarını hesaplayalım:

out vec3 FragPos;  
out vec3 Normal;
  
void main()
{
    gl_Position = projection * view * model * vec4(aPos, 1.0);
    FragPos = vec3(model * vec4(aPos, 1.0));
    Normal = aNormal;
}

Ve son olarak, fragment shader'a karşılık gelen in tipindeki değişkeni ekleyin:

in vec3 FragPos;  

Bu indeğişkeninde, parça başına dünya konumu olan FragPos vektörünü oluşturmak için üçgenin 3 dünya konumu vektöründen interpolasyon yapılacaktır. Artık gerekli tüm değişkenler ayarlandığına göre, aydınlatma hesaplamalarına başlayabiliriz.

Hesaplamamız gereken ilk şey, ışık kaynağı ile parçanın konumu arasındaki yön vektörüdür. Bir önceki bölümden, ışığın yön vektörünün, ışığın konum vektörü ile parçanın konum vektörü arasındaki fark vektörü olduğunu biliyoruz. Dönüşümler bölümünden de hatırlayacağınız gibi bu farkı her iki vektörü de birbirinden çıkararak kolayca hesaplayabiliriz. Ayrıca tüm ilgili vektörlerin birim vektörler olarak sonuçlandığından emin olmak istiyoruz, böylece hem normali hem de sonuçtaki yön vektörünü normalleştiririz:

vec3 norm = normalize(Normal);
vec3 lightDir = normalize(lightPos - FragPos);  

Işıklandırmayı hesaplarken genellikle bir vektörün büyüklüğü veya konumuyla ilgilenmeyiz; biz sadece onların yönünü önemsiyoruz. Sadece yönleriyle ilgilendiğimiz ve çoğu hesaplamayı basitleştirdiği için (nokta çarpımı gibi) neredeyse tüm hesaplamalar birim vektörlerle yapılır. Bu nedenle, ışıklandırma hesaplamaları yaparken, gerçek birim vektör olduklarından emin olmak için ilgili vektörleri her zaman normalleştirdiğinizden emin olun. Bir vektörü normalleştirmeyi unutmak yaygın bir hatadır.

Ardından, norm ve lightDir vektörleri arasındaki nokta çarpımını alarak ışığın mevcut parça üzerindeki dağınık etkisini hesaplamamız gerekiyor. Ortaya çıkan değer daha sonra ışığın rengiyle çarpılarak dağınık bileşen elde edilir, bu da her iki vektör arasındaki açı arttıkça daha koyu bir dağınık bileşenle sonuçlanır:

float diff = max(dot(norm, lightDir), 0.0);
vec3 diffuse = diff * lightColor;

Her iki vektör arasındaki açı 90 dereceden büyükse, o zaman nokta çarpımının sonucu aslında negatif olur ve negatif bir dağınık bileşen elde ederiz. Bu nedenle, dağınık bileşenin (ve dolayısıyla renklerin) asla negatif olmamasını sağlamak için her iki parametresinin en yüksek değerini döndüren max işlevini kullanırız. Negatif renkler için ışıklandırma tam olarak tanımlanmamıştır, bu nedenle, o eksantrik sanatçılardan biri değilseniz, bundan uzak durmak en iyisidir.

Artık hem bir ortam hem de dağınık bir bileşenimiz olduğuna göre, her iki rengi de birbirine ekliyoruz ve ardından elde edilen parçanın çıktı rengini elde etmek için sonucu nesnenin rengiyle çarpıyoruz:

vec3 result = (ambient + diffuse) * objectColor;
FragColor = vec4(result, 1.0);

Uygulamanız (ve tonlandırıcılarınız) başarıyla derlendiyse, şöyle bir şey görmelisiniz:

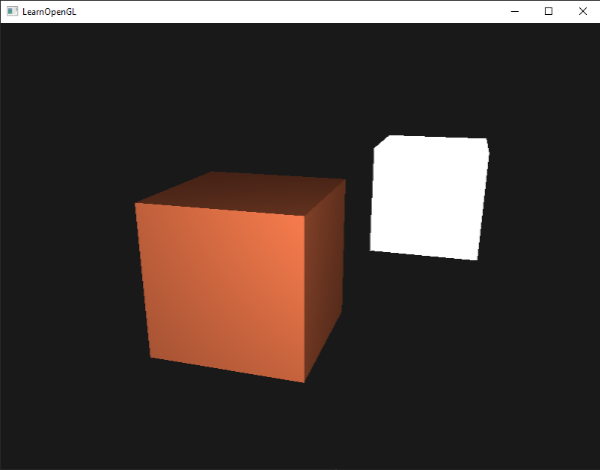
Dağınık ışıklandırma ile küpün yeniden gerçek bir küp gibi görünmeye başladığını görebilirsiniz. Normal vektörleri kafanızda görselleştirmeyi deneyin ve normal vektör ile ışığın yön vektörü arasındaki açı ne kadar büyük olursa, parçanın o kadar koyu olduğunu görmek için kamerayı küpün etrafında hareket ettirin.

Takılıp kalırsanız, kaynak kodunuzu buradaki tam kaynak kodla karşılaştırmaktan çekinmeyin.

Son bir şey

Önceki bölümde son iş olarak normal vektörü doğrudan vertex shader'dan fragment shader'a aktardık. Bununla birlikte, fragment shader'daki hesaplamaların tümü dünya uzayında yapılıyor, dolayısıyla normal vektörleri de dünya uzay koordinatlarına dönüştürmemiz gerekmez mi? Temelde evet, ancak bunu bir model matrisiyle çarpmak kadar basit değil.

İlk olarak, normal vektörler yalnızca yön vektörleridir ve uzayda belirli bir konumu temsil etmezler. İkincisi, normal vektörler homojen bir koordinata (vertex konumunun w bileşenine) sahip değildir. Bu, ötelemelerin normal vektörler üzerinde herhangi bir etkisinin olmaması gerektiği anlamına gelir. Dolayısıyla, normal vektörleri bir model matrisiyle çarpmak istiyorsak, model matrisinin sol üstteki 3x3'lük matrisini alarak matrisin öteleme kısmını kaldırmak isteriz (normal bir vektörün w bileşenini de şu şekilde ayarlayabileceğimize dikkat edin: 0 ve 4x4 matrisiyle çarpın).

İkincisi, eğer model matrisi uniform olmayan bir ölçek gerçekleştiriyorsa, vertex'ler, normal vektör artık yüzeye dik olmayacak şekilde değiştirilecektir. Aşağıdaki görüntü, böyle bir model matrisinin (uniform olmayan ölçeklendirmeye sahip) normal bir vektör üzerindeki etkisini göstermektedir:

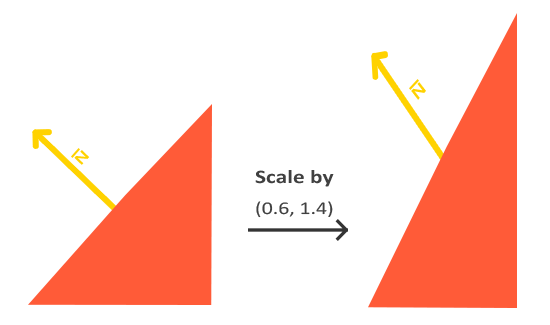
Uniform olmayan bir ölçek uyguladığımızda (not: uniform bir ölçek, normalin yönünü değil, yalnızca büyüklüğünü değiştirir; bu, normalleştirilerek kolayca sabitlenir), normal vektörler artık karşılık gelen yüzeye dik değildir ve bu da ışıklandırmayı bozar.

Bu davranışı düzeltmenin püf noktası, normal vektörler için özel olarak uyarlanmış farklı bir model matrisi kullanmaktır. Bu matrise normal matris denir ve normal vektörlerin yanlış ölçeklendirilmesinin etkisini ortadan kaldırmak için birkaç lineer cebirs işlemi kullanır. Bu matrisin nasıl hesaplandığını öğrenmek istiyorsanız buradaki makaleyi öneririm.

Normal matris "model matrisinin sol üst 3x3 kısmının tersinin transpozu" olarak tanımlanır. Bunun ne anlama geldiğini gerçekten anlamıyorsanız endişelenmeyin; henüz ters ve devrik matrisleri tartışmadık. Çoğu kaynağın normal matrisi model görünümü matrisinden türetilmiş olarak tanımladığını ancak dünya uzayında (görünüm uzayında değil) çalıştığımızdan onu model matrisinden türeteceğimizi unutmayın.

Vertex shader'da herhangi bir matris tipinde çalışan vertex shader'daki ters ve transpoze fonksiyonları kullanarak normal matrisi oluşturabiliriz. Öteleme özelliklerini kaybetmesini ve vec3 normal vektörüyle çarpılabilmesini sağlamak için matrisi 3x3'lük bir matrise dönüştürdüğümüzü unutmayın:

Normal = mat3(transpose(inverse(model))) * aNormal;  

Matrisleri ters çevirmek, shader'lar için maliyetli bir işlemdir; bu nedenle, sahnenizin her vertex'inde yapılması gerektiğinden, mümkün olduğunca ters işlemler yapmaktan kaçının. Öğrenme amacıyla bunu yapmak iyidir, ancak etkili bir uygulama için muhtemelen CPU'daki normal matrisi hesaplamak ve çizimden önce onu shader'a bir uniform aracılığıyla göndermek isteyeceksiniz (tıpkı model matrisi gibi).

Dağınık ışıklandırma bölümünde ışıklandırma iyiydi çünkü nesne üzerinde herhangi bir ölçeklendirme yapmadık, dolayısıyla normal bir matris kullanmaya gerçekten gerek yoktu ve normalleri model matrisiyle çarpmamız yeterliydi. Ancak uniform olmayan bir ölçek yapıyorsanız normal vektörlerinizi normal matrisle çarpmanız önemlidir.

Aynasal Işıklandırma

Eğer ışıklandırma konusundan hâlâ yorulmadıysanız, Phong aydınlatma modelini aynasal vurgular ekleyerek bitirmeye başlayabiliriz.

Dağınık ışıklandırmaya benzer şekilde, aynasal ışıklandırma, ışığın yön vektörünü ve nesnenin normal vektörlerini temel alır, ancak bu sefer aynı zamanda görüş yönünü de temel alır; oyuncunun fragment'a hangi yönden baktığı. Aynasal ışıklandırma yüzeylerin yansıtıcı özelliklerine dayanmaktadır. Nesnenin yüzeyini bir ayna olarak düşünürsek, yüzeye yansıyan ışığı gördüğümüz yerde aynasal ışık en güçlüdür. Bu etkiyi aşağıdaki resimde görebilirsiniz:

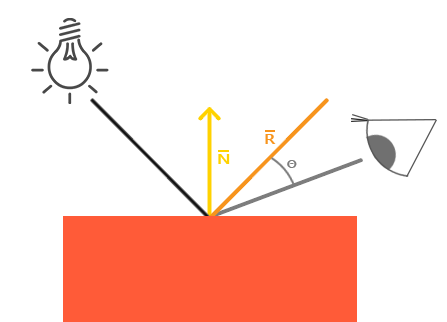
Işığın yönünü normal vektör etrafında yansıtarak bir yansıma vektörü hesaplıyoruz. Daha sonra bu yansıma vektörü ile görüş yönü arasındaki açısal mesafeyi hesaplıyoruz. Aralarındaki açı ne kadar yakınsa, aynasal ışığın etkisi de o kadar büyük olur. Ortaya çıkan etki, yüzeyden yansıyan ışığın yönüne baktığımızda bir miktar parlak nokta görmemizdir.

Görünüm vektörü, aynasal ışıklandırma için ihtiyacımız olan ekstra değişkenlerden biridir ve bunu, izleyicinin dünya uzayı konumunu ve fragment'in konumunu kullanarak hesaplayabiliriz. Daha sonra aynasal ışıklandırmanın yoğunluğunu hesaplıyoruz, bunu açık renkle çarpıyoruz ve bunu ortam ve yayılma bileşenlerine ekliyoruz.

Biz ışıklandırma hesaplamalarını dünya uzayında yapmayı seçtik ama çoğu insan ışıklandırmayı görüş uzayında yapmayı tercih ediyor. Görüntüleme alanının bir avantajı, izleyicinin konumunun her zaman (0,0,0) konumunda olmasıdır, böylece izleyicinin konumunu zaten serbestçe almış olursunuz. Ancak dünya uzayındaki ışıklandırmanın hesaplanmasını öğrenme amaçları açısından daha sezgisel buluyorum. Eğer hala görüş alanındaki ışıklandırmayı hesaplamak istiyorsanız, ilgili tüm vektörleri de görünüm matrisiyle dönüştürmek istiyorsunuz (normal matrisi de değiştirmeyi unutmayın).

İzleyicinin dünya uzay koordinatlarını elde etmek için kamera nesnesinin (tabii ki izleyicidir) konum vektörünü alırız. Öyleyse fragment shader'a başka bir uniform değişken ekleyelim ve kamera konumu vektörünü shader'a aktaralım:

uniform vec3 viewPos;

lightingShader.setVec3("viewPos", camera.Position); 

Artık gerekli tüm değişkenlere sahip olduğumuza göre aynasal yoğunluğu hesaplayabiliriz. İlk olarak, çok fazla bir etkiye sahip olmaması için, aynasal vurguya orta-parlak bir renk vermek üzere bir aynasal yoğunluk değeri tanımlarız:

float specularStrength = 0.5;

Eğer bunu 1.0f'ye ayarlarsak gerçekten parlak bir aynasal bileşen elde ederiz ki bu mercan renkli küp için biraz fazla. Bir sonraki bölümde tüm bu ışıklandırma yoğunluklarının doğru şekilde ayarlanmasından ve bunların nesneleri nasıl etkilediğinden bahsedeceğiz. Daha sonra görüş yönü vektörünü ve normal eksen boyunca karşılık gelen yansıma vektörünü hesaplıyoruz:

vec3 viewDir = normalize(viewPos - FragPos);
vec3 reflectDir = reflect(-lightDir, norm);  

lightDirvektörünü olumsuzladığımızı unutmayın. reflect işlevi, ilk vektörün ışık kaynağından fragment'in konumuna doğru işaret etmesini bekler, ancak lightDirvektörü şu anda tam tersini işaret etmektedir: fragment'tan ışık kaynağına doğru (bu, lightDir vektörünü hesapladığımızda daha önce yaptığımız çıkarma sırasına bağlıdır). Doğru reflect vektörünü elde ettiğimizden emin olmak için önce lightDirvektörünü olumsuzlayarak yönünü tersine çeviririz. İkinci argüman normal bir vektör beklediğinden normalleştirilmiş norm vektörünü sağlıyoruz.

O zaman yapılması gereken şey aslında aynasal bileşeni hesaplamaktır. Bu, aşağıdaki formülle gerçekleştirilir:

float spec = pow(max(dot(viewDir, reflectDir), 0.0), 32);
vec3 specular = specularStrength * spec * lightColor;  

Önce bakış yönü ile yansıma yönü arasındaki nokta çarpımını hesaplıyoruz (negatif olmadığından emin oluyoruz) ve ardından bunu 32'nin kuvvetine yükseltiyoruz. Bu 32değeri, parlak noktanın parlaklık değeridir. Bir cismin parlaklık değeri ne kadar yüksek olursa, ışığı etrafa dağıtmak yerine o kadar doğru yansıtır ve dolayısıyla parlak nokta da o kadar küçük olur. Aşağıda farklı parlaklık değerlerinin etkisini gösteren bir görsel bulunmaktadır:

Aynasal bileşenin çok fazla dikkat dağıtmasını istemediğimiz için üssü 32'de tutuyoruz. Yapılacak tek şey bunu ortam ve dağınık bileşenlere eklemek ve birleştirilmiş sonucu nesnenin rengiyle çarpmak:

vec3 result = (ambient + diffuse + specular) * objectColor;
FragColor = vec4(result, 1.0);

Artık Phong ışıklandırma modelinin tüm ışıklandırma bileşenlerini hesapladık. Bakış açınıza göre şöyle bir şey görmelisiniz:

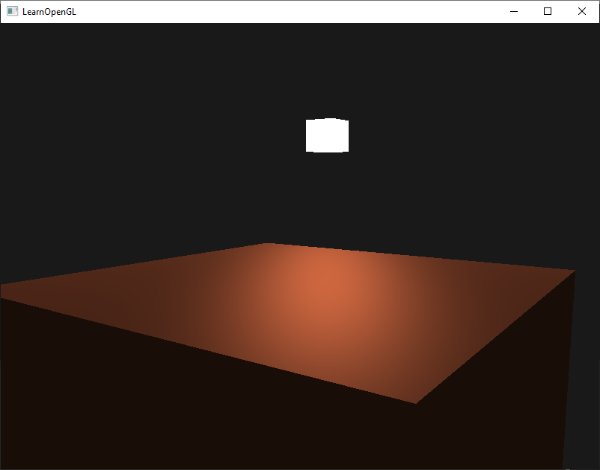
Uygulamanın kaynak kodunun tamamını burada bulabilirsiniz.

Işıklandırma shader'larının ilk zamanlarında, geliştiriciler vertex shader'da Phong ışıklandırma modelini uyguluyorlardı. Vertex shader'da ışıklandırma yapmanın avantajı, fragment'lara kıyasla genellikle çok daha az vertex olduğundan çok daha verimli olmasıdır, dolayısıyla (pahalı) ışıklandırma hesaplamaları daha az sıklıkta yapılır. Ancak vertex shader'da elde edilen renk değeri yalnızca o vertex'in ışıklandırma rengidir ve çevredeki fragment'ların renk değerleri de enterpolasyonlu ışıklandırma renklerinin sonucudur. Sonuç olarak, çok miktarda vertex kullanılmadığı sürece ışıklandırma pek gerçekçi olmuyordu:

Phong ışıklandırma modeli vertex shader'da uygulandığında buna Phong shader yerine Gouraud shader adı verilir. Enterpolasyon nedeniyle ışıklandırmanın biraz kapalı göründüğünü unutmayın. Phong shader çok daha düzgün ışıklandırma sağlar.

Şimdiye kadar shader'ların ne kadar güçlü olduğunu görmeye başlamış olmalısınız. Çok az bilgiyle shader'lar, ışığın tüm nesnelerimiz için fragment'in renklerini nasıl etkilediğini hesaplayabilir. Sonraki bölümlerde ışıklandırma modeliyle neler yapabileceğimizi daha derinlemesine inceleyeceğiz.

Alıştırmalar

• Şu anda ışık kaynağı, hareket etmeyen, sıkıcı, statik bir ışık kaynağıdır. Işık kaynağını zaman içinde sin veya cos kullanarak sahnenin etrafında hareket ettirmeye çalışın. Işıklandırmanın zaman içindeki değişimini izlemek, Phong'un ışıklandırma modeli: çözüm hakkında iyi bir anlayışa sahip olmanızı sağlar.

• Farklı ortam, yayılma ve aynasal güçlerle denemeler yapın ve bunların sonucu nasıl etkilediğini görün. Ayrıca parlaklık faktörünü de deneyin. Neden belirli değerlerin belirli bir görsel çıktıya sahip olduğunu anlamaya çalışın.

• Phong gölgelendirmesini dünya uzayı yerine görünüm uzayında yapın: çözüm.

• Phong gölgeleme yerine Gouraud gölgeleme uygulayın. Eğer işleri doğru yaptıysanız, küp nesnedeki ışıklandırma (özellikle aynasal vurgular) biraz daha bozuk görünmelidir. Neden bu kadar tuhaf göründüğüne dair mantık yürütmeye çalışın: çözüm.

Orijinal Kaynak: Basic Lighting

Çeviri: Nezihe Sözen