Dönüşümler

Artık nesneleri nasıl oluşturacağımızı, renklendireceğimizi ve dokuları kullanarak ayrıntılı bir görünüm vermeyi biliyoruz, ancak hepsi statik nesne olduğu için hâlâ çok ilginç bir görünüme sahip değiller. Köşe noktalarını değiştirerek ve her karesini arabellekleri yeniden yapılandırarak hareket ettirebiliriz, ancak bu hantal ve biraz işlem gücüne mâl oluyor. Bir nesneyi dönüştürmenin çok daha iyi yolları vardır ve bu da matris nesnelerini kullanmaktır.

Matrisler, ilk başta korkutucu görünen çok güçlü matematiksel yapılardır, ancak bunlara alıştıktan sonra son derece yararlı olduklarını görürüz. Matrisleri tartışırken, matematiğe küçük bir dalış yapmamız gerekecek ve matematiğe meraklı okuyucular için de daha fazla okuma yapmaları için ek kaynaklar yayınlayacağım.

Bununla birlikte, dönüşümleri tam olarak anlamak için, matrislere başlamadan önce vektörlere biraz daha derinlemesine bakmamız gerekir. Bu bölümün odak noktası, daha sonra ihtiyaç duyacağımız konularda size temel bir matematiksel altyapı sağlamaktır. Konular zorsa, bunları olabildiğince anlamaya çalışın ve kavramları ihtiyacınız olduğunda gözden geçirmek için daha sonra bu bölüme yine dönün.

Vektörler

En basit anlamda vektörler, yönden başka bir şey değildir. Bir vektörün bir yönü ve büyüklüğü (kuvveti veya uzunluğu olarak da bilinir) vardır. Vektörleri bir define haritasında yönler gibi düşünebilirsiniz: 10 adım sola git, şimdi 3 adım kuzeye git ve 5 adım sağa git; burada 'sol' yön ve '10 adım' vektörün büyüklüğüdür. Define haritasının yönleri 3 vektör içerir. Vektörler herhangi bir boyuta sahip olabilir, ancak genellikle 2 ila 4 boyutlarıyla çalışırız. Bir vektör 2 boyuta sahipse, bir düzlemde bir yönü temsil eder (2-boyutlu grafikleri düşünün) ve 3 boyutu olduğunda 3-boyutlu dünyada herhangi bir yönü temsil edebilir .

Aşağıda, 2-boyutlu bir grafikte her birinin (x, y) ile temsil ediildiği 3 adet vektör göreceksiniz. Vektörleri 3B yerine 2B'de görüntülemek daha kolay olduğundan, 2B vektörleri z koordinatı 0 olan 3B vektörler olarak düşünebilirsiniz. Vektörler yönleri temsil ettiğinden, vektörün orijin değerini değiştirmez. Aşağıdaki grafikte, orijinleri farklı olmasına rağmen $\color{red}{\bar{v}}$ ve $\color{blue}{\bar{w}}$ değerlerinin eşit olduğunu görebiliriz:

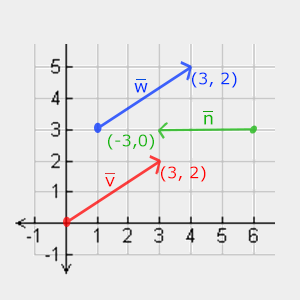
Vektörler tanımlanırken matematikçiler genellikle vektörleri, $\bar{v}$ şeklinde başlarında küçük bir çizgili semboller olarak tanımlamayı tercih ederler. Ayrıca, vektörleri formüllerde görüntülerken aşağıdaki gibi görünür:

$$\bar{v} = \begin{pmatrix} \color{red}x \\ \color{green}y \\ \color{blue}z \end{pmatrix}$$

Vektörler yön olarak belirtildiğinden, konum olarak görselleştirmek bazen zordur. Vektörleri konum olarak görselleştirmek istersek, yön vektörünün orijinini (0,0,0) olarak hayal edebilir ve ardından noktayı belirten belirli bir yöne doğru işaret edebilir, bunu da konum vektörü yapabiliriz (farklı bir orijin belirleyebiliriz ve sonra şunu söyleyebiliriz: "Bu vektör uzayda bu noktayı işaret eder"). Konum vektörü (3,5), (0,0) orijinli grafik üzerinde (3,5)' i gösterir. Vektörleri kullanarak 2-boyutlu ve 3-boyutlu uzayda yönleri ve konumları tanımlayabiliriz.

Tıpkı normal sayılar üzerinde olduğu gibi, vektörler üzerinde de (bazılarını daha önce gördüğünüz) birkaç işlem tanımlayabiliriz.

Skaler (Yönsüz) Vektör İşlemleri

Skaler tek bir rakamdır. Bir skaler ile bir vektörü toplarken/ çıkarırken / çarparken veya bölerken, vektörün her bir elemanını skaler ile toplar / çıkarır / çarparız veya böleriz. Bu durum şöyle görünecektir:

$$\begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix} + x \rightarrow \begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix} + \begin{pmatrix} x \\ x \\ x \end{pmatrix} = \begin{pmatrix} \color{red}1 + x \\ \color{green}2 + x \\ \color{blue}3 + x \end{pmatrix}$$

Where+ can be+,−,⋅ or÷ where⋅ is the multiplication operator.

$+$ operatörü $-$ , $\cdot$ ya da $\div$ olabilmektedir ki $\cdot$ çarpım operatörüdür.

Vektör Olumsuzlama (ing. Vector Negation)

Bir vektörün olumsuzlanması, ters yönde bir vektör biçimine getirilmesi demektir. Kuzey-doğuyu işaret eden bir vektör, olumsuzlamadan sonra güney-batıya bakacaktır. Bir vektörü olumsuzlamak için her bir bileşene eksi işareti koyarız (bunu skaler -1 değeri ile yapılan skaler-vektör çarpımı olarak da düşünebilirsiniz):

$$-\bar{v} = -\begin{pmatrix} \color{red}{v_x} \\ \color{blue}{v_y} \\ \color{green}{v_z} \end{pmatrix} = \begin{pmatrix} -\color{red}{v_x} \\ -\color{blue}{v_y} \\ -\color{green}{v_z} \end{pmatrix}$$

Toplama ve Çıkarma

İki vektörün toplanması bileşen bazında toplama olarak tanımlanır, yani bir vektörün her bileşeni diğer vektörün aynı bileşenine şu şekilde eklenir:

$$\bar{v} = \begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix}, \bar{k} = \begin{pmatrix} \color{red}4 \\ \color{green}5 \\ \color{blue}6 \end{pmatrix} \rightarrow \bar{v} + \bar{k} = \begin{pmatrix} \color{red}1 + \color{red}4 \\ \color{green}2 + \color{green}5 \\ \color{blue}3 + \color{blue}6 \end{pmatrix} = \begin{pmatrix} \color{red}5 \\ \color{green}7 \\ \color{blue}9 \end{pmatrix}$$

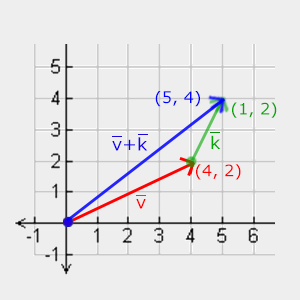
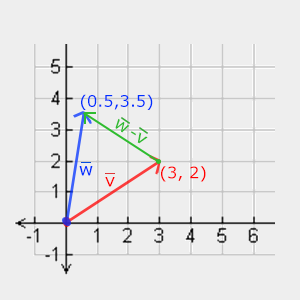
Tıpkı normal toplama ve çıkarma gibi, vektör çıkarma da olumsuzlanmış vektörle toplama ile aynıdır:

$$\bar{v} = \begin{pmatrix} \color{red}{1} \\ \color{green}{2} \\ \color{blue}{3} \end{pmatrix}, \bar{k} = \begin{pmatrix} \color{red}{4} \\ \color{green}{5} \\ \color{blue}{6} \end{pmatrix} \rightarrow \bar{v} + -\bar{k} = \begin{pmatrix} \color{red}{1} + (-\color{red}{4}) \\ \color{green}{2} + (-\color{green}{5}) \\ \color{blue}{3} + (-\color{blue}{6}) \end{pmatrix} = \begin{pmatrix} -\color{red}{3} \\ -\color{green}{3} \\ -\color{blue}{3} \end{pmatrix}$$

İki vektörün birbirinden çıkarılması, her iki vektörün işaret ettiği konumların farkı olan bir vektördür. Bu, iki nokta arasındaki fark olan bir vektörü elde etmemiz gereken bazı durumlarda faydalı olmaktadır.

Uzunluk

Bir vektörün uzunluğunu/ büyüklüğünü elde etmek için matematik derslerinizden hatırlayabileceğiniz Pisagor teoremini kullanırız.

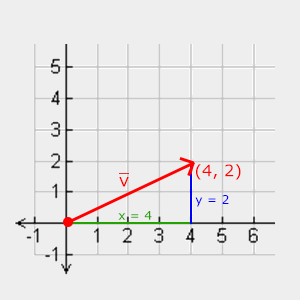
İki kenarın (x, y) değerleri bilindiğinden ve eğimli kenar olan $\color{red}{\bar{v}}$ 'nin uzunluğunu bilmek istediğimizden, Pisagor teoremini kullanarak bunu hesaplayabiliriz:

$$||\color{red}{\bar{v}}|| = \sqrt{\color{green}x^2 + \color{blue}y^2}$$

$||\color{red}{\bar{v}}||$gösterimi ile $\color{red}{\bar{v}}$ vektörünün uzunluğu ifade edilmektedir . Bu denkleme$z^2$eklenerek kolayca 3-boyutlu dünya için genişletilebilir. Aşağıdaki denklemde(4, 2) vektörünün uzunluğunun nasıl hesaplandığı görülmektedir:

$$||\color{red}{\bar{v}}|| = \sqrt{\color{green}4^2 + \color{blue}2^2} = \sqrt{\color{green}16 + \color{blue}4} = \sqrt{20} = 4.47$$

Sonuç 4.47olmaktadır.

Birim vektör olarak adlandırdığımız özel bir vektör türü de bulunmaktadır. Bir birim vektör uzunluğunun tam olarak 1 olması gibi bir özelliğe sahiptir. Vektörün bileşenlerinin her birini uzunluğuna bölerek herhangi bir vektörden birim vektör $\hat{n}$ 'i hesaplayabiliriz:

$$\hat{n} = \frac{\bar{v}}{||\bar{v}||}$$

Buna bir vektörü normalleştirme denir. Birim vektörler, başlarının üstünde küçük bir çatı ile gösterilir ve özellikle sadece yönlerini önemsediğimizde (genellikle bir vektörün uzunluğunu değiştirirsek yön değişmez) çalışmak daha kolaydır.

Vektör- Vektör Çarpımı

İki vektörün çarpım işlemi biraz ilginçtir. Normal çarpma işlemi görsel olarak hiçbir anlam ifade etmediği için vektörlerde tam olarak tanımlanmamıştır, ancak seçebileceğimiz iki özel durumumuz vardır: biri $\bar{v} \cdot \bar{k}$ ile gösterilen iç çarpım (ing. dot product) ve diğeri $\bar{v} \times \bar{k}$ ile gösterilen çapraz çarpım (ing. cross product).

İç çarpım (ing. Dot product)

İki vektörün iç çarpımı, uzunluklarının skaler çarpımlarının aralarındaki açının kosinüsü ile çarpımına eşittir. Bu kafa karıştırıcı geliyorsa formülüne bir göz atın:

$$\bar{v} \cdot \bar{k} = ||\bar{v}|| \cdot ||\bar{k}|| \cdot \cos \theta$$

Aralarındaki açı teta (θ) olarak temsil edilmiştir. Peki bu neden önemlidir? Eğer $\bar{v}$ ve $\bar{k}$ birim vektörler ise uzunluklarının 1'e eşit olacağını düşünün. Bu, formülü etkili bir şekilde kısaltacaktır:

$$\hat{v} \cdot \hat{k} = 1 \cdot 1 \cdot \cos \theta = \cos \theta$$

İç çarpım sadece her iki vektör arasındaki açıyı tanımlıyor. Açı 90 derece olduğunda cosişlevinin 0 ile sonuçlandığını; açı 0 olduğunda cosişlevinin 1 ile sonuçlandığını hatırlayabilirsiniz. Bu bilgi, iki vektörün iç çarpımını kullanarak birbirine dik veya birbirine paralel olup olmadığını kolayca test etmemizi sağlar (dikey vektörler birbirine dik açılıdır). sinveya cosişlevleri hakkında daha fazla bilgi edinmek isterseniz, temel trigonometri içeren Khan Academy videolarını öneririm .

Birim olmayan iki vektör arasındaki açıyı da hesaplayabilirsiniz, ancak her iki vektörün uzunluğunu $cos \theta$ ile hesaplanacak olan sonuca bölmeniz gerekir.

Peki iç çarpımı nasıl hesaplıyoruz? İç çarpım, sonuçlarını hep birlikte topladığımız, bileşen bazında bir çarpmadır.

$$\begin{pmatrix} \color{red}{0.6} \\ -\color{green}{0.8} \\ \color{blue}0 \end{pmatrix} \cdot \begin{pmatrix} \color{red}0 \\ \color{green}1 \\ \color{blue}0 \end{pmatrix} = (\color{red}{0.6} * \color{red}0) + (-\color{green}{0.8} * \color{green}1) + (\color{blue}0 * \color{blue}0) = -0.8$$

Her iki birim vektör arasındaki dereceyi hesaplamak için kosinüs işlevinin tersini $cos^{-1}$ kullanırız ki bu da 143.1 derece ile sonuçlanıyor. İiki vektör arasındaki açıyı etkili bir şekilde hesapladık. İç çarpım, daha sonra ışıklandırma hesaplamaları yaparken bize çok faydalı olacaktır.

Çapraz Çarpım (ing. Cross product)

Çapraz çarpım sadece 3-boyutlu uzayda tanımlanır. İki paralel olmayan vektörü girdi olarak alır ve her iki giriş vektörüne dik olan üçüncü bir vektör üretir. Her iki giriş vektörü de dikse, çapraz çarpım 3 dik vektörle sonuçlanır; bu bilgi ilerideki bölümlerde faydalı olacaktır. Aşağıdaki görsel bunun 3B uzayda neye benzediğini göstermektedir:

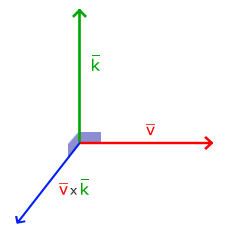
Diğer işlemlerin aksine, çapraz çarpım lineer cebire girmeden gerçekten kolay anlaşılabilir değildir, bu yüzden formülü ezberlemek en iyisidir. Aşağıda iki dikey A ve B vektörü arasındaki çapraz çarpım işlemini göreceksiniz:

$$\begin{pmatrix} \color{red}{A_{x}} \\ \color{green}{A_{y}} \\ \color{blue}{A_{z}} \end{pmatrix} \times \begin{pmatrix} \color{red}{B_{x}} \\ \color{green}{B_{y}} \\ \color{blue}{B_{z}} \end{pmatrix} = \begin{pmatrix} \color{green}{A_{y}} \cdot \color{blue}{B_{z}} - \color{blue}{A_{z}} \cdot \color{green}{B_{y}} \\ \color{blue}{A_{z}} \cdot \color{red}{B_{x}} - \color{red}{A_{x}} \cdot \color{blue}{B_{z}} \\ \color{red}{A_{x}} \cdot \color{green}{B_{y}} - \color{green}{A_{y}} \cdot \color{red}{B_{x}} \end{pmatrix}$$

Gördüğünüz gibi, gerçekten mantıklı görünmüyor; ancak, lineer cebirde bu adımları izlerseniz giriş vektörlerinizle dikey olan başka bir vektör elde edersiniz.

Matrisler

Şimdi, vektörler için neredeyse her şeyi tartıştığımıza göre, matrisleri inceleme zamanı! Bir matris dikdörtgen bir sayı dizisi, sembol ve/ veya matematiksel ifadelerdir. Bir matristeki her bir öğeye matrisin elemanı denir. 2x3'lük bir matris örneği aşağıda gösterilmiştir:

$$\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}$$

Matrisler, i'nin satır ve j'nin sütun olduğu (i,j) ile indislenir, bu nedenle yukarıdaki matrise 2x3 matrisi denir (3 sütun ve 2 satır olduğundan). Bu durum, 2-boyutlu grafikleri (x,y) olarak indislerken alışık olduğunuz şeyin tersidir. 4 değerini almak için (2,1) olarak dizine ekleriz (ikinci satır, ilk sütun) .

Matrisler temel olarak bundan başka bir şey değildir, sadece matematiksel ifadelerin dikdörtgen dizileridir. Çok güzel matematiksel özelliklere sahiptirler ve tıpkı vektörlerde olduğu gibi matrisler üzerinde toplama, çıkarma ve çarpma işlemleri tanımlayabiliriz.

Toplama ve Çıkarma

İki matris arasındaki toplama ve çıkarma işlemi her bir eleman temelinde yapılır. Dolayısıyla, normal sayılar için aşina olduğumuz, ancak aynı indise sahip her iki matrisin elemanları için uygulayabileceğimiz genel kurallar geçerlidir. Bu, toplama ve çıkarma işleminin yalnızca aynı boyutlardaki matrisler için tanımlandığı anlamına gelir. 3x2 matrisi ve 2x3 matrisi (veya 3x3 matrisi ve 4x4 matrisi) birlikte eklenemez ve çıkarılamaz. Matrislerde toplama işleminin iki adet 2x2'lik matris üzerinde nasıl uygulandığını görelim:

$$\begin{bmatrix} \color{red}1 & \color{red}2 \\ \color{green}3 & \color{green}4 \end{bmatrix} + \begin{bmatrix} \color{red}5 & \color{red}6 \\ \color{green}7 & \color{green}8 \end{bmatrix} = \begin{bmatrix} \color{red}1 + \color{red}5 & \color{red}2 + \color{red}6 \\ \color{green}3 + \color{green}7 & \color{green}4 + \color{green}8 \end{bmatrix} = \begin{bmatrix} \color{red}6 & \color{red}8 \\ \color{green}{10} & \color{green}{12} \end{bmatrix}$$

Matrislerde çıkarma işlemi için aynı kurallar geçerlidir:

$$\begin{bmatrix} \color{red}4 & \color{red}2 \\ \color{green}1 & \color{green}6 \end{bmatrix} - \begin{bmatrix} \color{red}2 & \color{red}4 \\ \color{green}0 & \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}4 - \color{red}2 & \color{red}2 - \color{red}4 \\ \color{green}1 - \color{green}0 & \color{green}6 - \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & -\color{red}2 \\ \color{green}1 & \color{green}5 \end{bmatrix}$$

Matris-skaler çarpımı

Bir matris-skaler çarpım işlemi, matrisin her elemanını bir skaler ile çarpmaktadır. Aşağıdaki örnek çarpma işleminin nasıl uygulandığını göstermektedir:

$$\color{green}2 \cdot \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} \color{green}2 \cdot 1 & \color{green}2 \cdot 2 \\ \color{green}2 \cdot 3 & \color{green}2 \cdot 4 \end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 6 & 8 \end{bmatrix}$$

Ayrıca bu tek sayıların neden skaler olarak adlandırıldığı önemlidir. Bir skaler, temel olarak matrisin tüm elemanlarını kendi değerine göre ölçeklendirir. Önceki örnekte, tüm elemanlar 2 ile ölçeklendirildi.

Şimdiye kadarki tüm uygulamalarımız gerçekten çok karmaşık değildi. Yani, matris-matris çarpımına başlayana dek...

Matris- matris çarpımı

Matrisleri çarpmak her zaman karmaşık olmakla kalmaz, rahat etmek de oldukça zordur. Matris çarpımı temel olarak, çarpma sırasında önceden tanımlanmış bir dizi kurala uymak anlamına da gelir. Yine de birkaç kısıtlama vardır:

1. Yalnızca sol taraftaki matristeki sütun sayısı sağ taraftaki matristeki satır sayısına eşitse iki matrisi çarpabilirsiniz.

2. Matris çarpımı değişme özelliğine sahip değildir. $A \cdot B \neq B \cdot A$

2x2 'lık iki matrisin çarpım örneğini inceleyelim:

$$\begin{bmatrix} \color{red}1 & \color{red}2 \\ \color{green}3 & \color{green}4 \end{bmatrix} \cdot \begin{bmatrix} \color{blue}5 & \color{purple}6 \\ \color{blue}7 & \color{purple}8 \end{bmatrix} = \begin{bmatrix} \color{red}1 \cdot \color{blue}5 + \color{red}2 \cdot \color{blue}7 & \color{red}1 \cdot \color{purple}6 + \color{red}2 \cdot \color{purple}8 \\ \color{green}3 \cdot \color{blue}5 + \color{green}4 \cdot \color{blue}7 & \color{green}3 \cdot \color{purple}6 + \color{green}4 \cdot \color{purple}8 \end{bmatrix} = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix}$$

Şu anda muhtemelen neler olduğunu anlamaya çalışıyorsunuz. Matris çarpımı, soldaki matrisin satırlarını sağdaki matrisin sütunlarıyla normal çarpma ve toplama işlemlerinin bir birleşimidir. Bunu aşağıdaki görüntü ile tartışmayı deneyelim:

Önce soldaki matrisin üst sırasını alıyoruz ve sonra sağdaki matristen bir sütun alıyoruz. Seçtiğimiz satır ve sütun, elde edilen 2x2 matrisinin hangi çıktı değerini hesaplayacağımıza etki ediyor. Soldaki matrisin ilk satırını alırsak, sonuç değeri sonuç matrisinin ilk satırında kalır, yani ilk sütunun sonuç değeri sonuç matrisinin ilk sütununda biter . Bu tam olarak kırmızı ile çevrelenmiş kısım için geçerlidir. Sağ alttaki (yeşil renk ile çevrili) sonucu hesaplamak için birinci matrisin alt satırını ve ikinci matrisin en sağdaki sütununu alırız.

Ortaya çıkan değeri hesaplamak için, satır ve sütunun ilk elemanını normal çarpma işlemi kullanarak çarparız, ikinci elemanlar, üçüncü, dördüncü vb. için de aynısını yaparız. Tek tek çarpmaların sonuçları toplanır ve sonucumuz elde edilir. Gereksinimlerden birinin sol matris sütunlarının ve sağ matris satırlarının boyutlarının eşit olması şimdi sizlere mantıklı gelmiştir, aksi takdirde işlemleri bitiremezdik!

Sonuç, n'nin sol taraftaki matrisin satır sayısı olduğu ve m 'nin de sağ taraftaki matrisin sütun sayısı olduğu (n,m) boyutlarına sahip bir matristir.

Çarpımları hayal etmekte zorluk çekiyorsanız endişelenmeyin. Hesaplamaları elle yapmaya çalışın ve zorlandığınızda bu sayfaya geri dönün. Zamanla, matris çarpımı sizin için alışkanlık hâline gelir.

Daha büyük bir örnekle matris-matris çarpımı tartışmasını bitirelim. Renkleri kullanarak örüntüyü görselleştirmeye çalışın. Yararlı bir alıştırma olarak, çarpma ile ilgili kendi cevabınızı bulup bulamayacağınıza bakın ve sonra bunları sonuçtaki matrisle karşılaştırın (elle bir matris çarpımı yapmaya çalıştığınızda, bunları hızlıca kavrayacaksınız).

$$\begin{bmatrix} \color{red}4 & \color{red}2 & \color{red}0 \\ \color{green}0 & \color{green}8 & \color{green}1 \\ \color{blue}0 & \color{blue}1 & \color{blue}0 \end{bmatrix} \cdot \begin{bmatrix} \color{red}4 & \color{green}2 & \color{blue}1 \\ \color{red}2 & \color{green}0 & \color{blue}4 \\ \color{red}9 & \color{green}4 & \color{blue}2 \end{bmatrix} = \begin{bmatrix} \color{red}4 \cdot \color{red}4 + \color{red}2 \cdot \color{red}2 + \color{red}0 \cdot \color{red}9 & \color{red}4 \cdot \color{green}2 + \color{red}2 \cdot \color{green}0 + \color{red}0 \cdot \color{green}4 & \color{red}4 \cdot \color{blue}1 + \color{red}2 \cdot \color{blue}4 + \color{red}0 \cdot \color{blue}2 \\ \color{green}0 \cdot \color{red}4 + \color{green}8 \cdot \color{red}2 + \color{green}1 \cdot \color{red}9 & \color{green}0 \cdot \color{green}2 + \color{green}8 \cdot \color{green}0 + \color{green}1 \cdot \color{green}4 & \color{green}0 \cdot \color{blue}1 + \color{green}8 \cdot \color{blue}4 + \color{green}1 \cdot \color{blue}2 \\ \color{blue}0 \cdot \color{red}4 + \color{blue}1 \cdot \color{red}2 + \color{blue}0 \cdot \color{red}9 & \color{blue}0 \cdot \color{green}2 + \color{blue}1 \cdot \color{green}0 + \color{blue}0 \cdot \color{green}4 & \color{blue}0 \cdot \color{blue}1 + \color{blue}1 \cdot \color{blue}4 + \color{blue}0 \cdot \color{blue}2 \end{bmatrix} \\ = \begin{bmatrix} 20 & 8 & 12 \\ 25 & 4 & 34 \\ 2 & 0 & 4 \end{bmatrix}$$

Gördüğünüz gibi, matris-matris çarpımı oldukça külfetli bir süreçtir ve hatalara çok açıktır (bu yüzden genellikle bilgisayarların bunu yapmasını isteriz) ve matrisler büyüdüğünde bu sorunlu gerçek hız kazanır. Daha fazlası için istekliyseniz ve matrislerin matematiksel özelliklerinden biraz daha fazlasını merak ediyorsanız, bu Khan Academy videolarına matrisler hakkında göz atmanızı şiddetle tavsiye ederim.

Artık matrisleri nasıl çarpacağımızı bildiğimize göre, iyi yerlere ulaşmaya başlayabiliriz.

Matris- Vektör Çarpımı

Şimdiye kadar adil bir vektör paylaşımımız vardı. Bunları konumları, renkleri ve hatta doku koordinatlarını temsil etmek için kullandık. Labirentimizden çıkalım ve bir vektörün temel olarak bir Nx1 matrisi olduğunu söyleyelim. Burada N, vektörün bileşen sayısıdır (N-boyutlu vektör olarak da bilinir). Düşünürseniz, çok mantıklı... Vektörler, matrisler gibi bir sayı dizisidir, ancak sadece 1 sütun içerir. Peki, bu yeni bilgi bize nasıl yardımcı olacak? Bir MxN matrisimiz varsa, bu matrisi Nx1 vektörümüzle çarpabiliriz, çünkü matrisin sütunları vektörün satır sayısına eşittir, bu sayede matris çarpımı tanımlanır.

Peki matrisleri bir vektörle çarpabilmeyi neden önemsiyoruz? Öyle ki, bir matrisin içine yerleştirebileceğimiz birçok 2-boyutlu veya 3-boyutlu dönüşümler var ve bu matrisi bir vektörle çarpmak o vektörü dönüştürür. Hâlâ biraz kafanız karışıksa, birkaç örnekle devam edelim ve yakında ne demek istediğimizi anlayabileceksiniz.

Birim Matris

OpenGL' de genellikle birkaç sebepten 4x4 dönüşüm matrisleri ile çalışırız ve bu sebeplerden biri vektörlerin çoğunun 4 boyutunda olmasıdır. Düşünebileceğimiz en basit dönüşüm matrisi, birim matrisidir. Birim matrisi, köşegen dışında sadece 0'ları olan bir NxN matrisidir. Gördüğünüz gibi, bu dönüşüm matrisi bir vektörü tamamen zarar vermeden bırakıyor:

$$\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} = \begin{bmatrix} \color{red}1 \cdot 1 \\ \color{green}1 \cdot 2 \\ \color{blue}1 \cdot 3 \\ \color{purple}1 \cdot 4 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix}$$

Vektöre hiç dokunulmamış. Bu çarpma kurallarından anlaşılıyor ki ilk sonuç elemanı, matrisin ilk satırının her bir elemanının vektörün her bir elemanıyla çarpımıdır. Satır öğelerinin her biri birincisi hariç 0 olduğundan, şunu elde ediyoruz: $\color{red}1\cdot\color{black}1 + \color{red}0\cdot\color{black}2 + \color{red}0\cdot\color{black}3 + \color{red}0\cdot\color{black}4 =\color{black} 1$ ve bu durumun aynısı vektörün diğer 3 elemanı için de geçerlidir.

Dönüşemeyen bir dönüşüm matrisinin kullanımının ne olduğunu merak ediyor olabilirsiniz? Birim matris genellikle diğer dönüşüm matrislerini üretmek için bir başlangıç noktasıdır ve eğer lineer cebirde daha da derinlere inersek, teoremleri kanıtlamak ve lineer denklemleri çözmek için çok yararlı bir matristir.

Ölçekleme (ing. Scaling)

Bir vektörü ölçeklendirirken, okun uzunluğunu ölçeklendirmek istediğimiz miktarda artırarak yönünü aynı tutarız. 2 veya 3 boyutta çalıştığımızdan ölçeklendirmeyi, her biri ayrı bir ekseni (x, y ya daz) ölçeklendiren 2 veya 3 ölçekleme değişkeninden oluşan bir vektörle tanımlayabiliriz.

$\color{red}{\bar{v}} = (3,2)$ vektörünü ölçeklendirmeyi deneyelim. Vektörü x- ekseni boyunca0.5 oranında ölçeklendireceğiz, böylece iki kat daha dar hale getireceğiz ve vektörü y- ekseni boyunca2 ölçeklendiririz, bu da onu iki kat daha yüksek yapar. Vektörü $\color{blue}{\bar{s}}$ ifade edersek ve(0.5,2) ölçeklendirirsek nasıl göründüğüne bir bakalım:

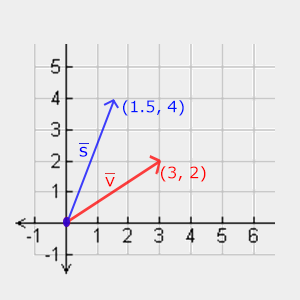
OpenGL' in genellikle 3- boyutlu alanda çalıştığını ve 2- boyutlu olduğu durumda z- ekseni ölçeğini1olarak ayarlayabildiğimizi unutmayın. Daha önce gerçekleştirdiğimiz ölçeklendirme işlemi eşit olmayan bir ölçektir, çünkü ölçeklendirme faktörü her eksen için aynı değildi. Skaler değer tüm eksenlerde eşit olacaksa, buna tek tip (ing. uniform) ölçek denir.

Bizim için ölçeklendirmeyi yapan bir dönüşüm matrisi oluşturmaya başlayalım. Birim matristen, köşegen elemanlarının her birinin karşılık gelen vektör elemanı ile çarpıldığını gördük. Birim matristeki 1'leri 3'lerle değiştirsek ne olur? Bu durumda, vektör öğelerinin her birini3değeriyle çarparak vektörü etkin bir şekilde3ile ölçeklendiririz. Ölçekleme değişkenlerini $(\color{red}{S_1}, \color{green}{S_2}, \color{blue}{S_3})$ olarak temsil edersek, herhangi bir vektörde $(x,y,z)$ ölçeklendirme matrisini şu şekilde tanımlayabiliriz:

$$\begin{bmatrix} \color{red}{S_1} & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}{S_2} & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}{S_3} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{S_1} \cdot x \\ \color{green}{S_2} \cdot y \\ \color{blue}{S_3} \cdot z \\ 1 \end{pmatrix}$$

Dördüncü ölçeklendirme değeri olan1'i koruduğumuza dikkat edin. w bileşeni, daha sonra göreceğimiz başka amaçlar için kullanılır.

Öteleme (ing.Translation)

Öteleme, farklı bir konuma sahip yeni bir vektör elde etmek için orijinal vektörünün üstüne başka bir vektörü ekleme, böylece vektörü bir öteleme vektörüne göre taşıma işlemidir. Vektörlerde toplama işlemini zaten tartıştık, bu yüzden sizler için çok yeni olmayacaktır.

Ölçekleme matrisi gibi, 4'e 4 matriste belirli işlemleri gerçekleştirmek için kullanabileceğimiz ve öteleme için 4. sütunun ilk 3 değeri olan çeşitli konumlar vardır. Öteleme vektörünü $(\color{red}{T_x},\color{green}{T_y},\color{blue}{T_z})$ olarak temsil edersek, öteleme matrisini şu şekilde tanımlayabiliriz:

$$\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}{T_x} \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}{T_y} \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}{T_z} \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x + \color{red}{T_x} \\ y + \color{green}{T_y} \\ z + \color{blue}{T_z} \\ 1 \end{pmatrix}$$

Tüm öteleme değerleri vektörün w sütunu ile çarpıldığı ve vektörün orijinal değerlerine eklendiği için işe yaramaktadır (matris çarpma kurallarını unutmayın). Bu, 3'e 3'lük bir matris ile mümkün olmazdı.

Homojen Koordinatlar Bir vektörünwbileşeni, homojen bir koordinat olarak da bilinir. 3- boyutlu vektörü homojen bir vektörden elde etmek içinx, y vez koordinatlarınıw koordinatlarına böleriz. Genelliklewbileşeni1.0 olduğu için bunu fark etmiyoruz. Homojen koordinatlar kullanmanın çeşitli avantajları vardır: 3- boyutlu vektörlerde matris öteleme yapmamıza izin verir (w bileşeni olmadan vektörleri öteleyemeyiz) ve sonraki bölümde 3- boyutlu perspektif oluşturmak için dew değerini kullanacağız. Ayrıca, homojen koordinat0'a eşit olduğunda, w koordinatı0 olan bir vektör ötelenemediğinden, vektör bir yön vektörü olarak bilinir.

Bir öteleme matrisi ile 3 eksenden (x, y, z) herhangi birindeki nesneleri taşıyabiliriz, bu da onu dönüştürme araç setimiz için çok kullanışlı bir dönüşüm matrisi haline getirir.

Döndürme (ing. Rotation)

Son birkaç dönüşümün 2- boyutlu veya 3- boyutlu uzayda anlaşılması ve görselleştirilmesi nispeten kolaydı, ancak dönüşler biraz daha zordur. Bu matrislerin nasıl oluşturulduğunu tam olarak bilmek istiyorsanız, Khan Academy' nin lineer cebir videolarının dündürme başlıklarını izlemenizi tavsiye ederim.

İlk önce bir vektörün dönüşünün gerçekte ne olduğunu tanımlayalım. İkinci boyutta veya üçüncü boyutta bir dönüş bir açı ile temsil edilir. Bir açı, tüm bir dairenin 360 derece veya 2 PI radyana sahip olduğu derece veya radyan cinsinden olabilir. Genellikle daha alışık olduğumuz için dereceleri kullanarak döndürmeyi açıklamayı tercih ederim.

Çoğu döndürme işlevi radyan cinsinden bir açı kullanır, ama neyse ki dereceler kolayca radyana dönüştürülebiliyor: derece cinsinden açı = radyan cinsinden açı * (180 / PI) radyan cinsinden açı = derece cinsinden açı * (PI / 180) PI sayısı (yuvarlanarak) 3.14159265359eşit olduğunda.

Yarım dairenin döndürülmesi, bizi 360/2 = 180 derece döndürür ve 1/ 5'i sağa döndürmek 360/5 = 72 derece sağa döndüğümüz anlamına gelir. Bu, $\color{red}{\bar{v}}$ 'in $\color{green}{\bar{k}}$ den 72 derece sağa veya saat yönünde döndürüldüğü temel bir 2- boyutlu vektör için gösterilmiştir:

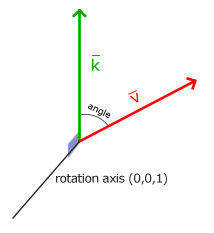
3B' deki döndürmeler bir açı ve bir döndürme ekseni ile belirtilir. Belirtilen açı, nesneyi dönüş ekseni boyunca döndürür. Sürekli olarak tek bir dönme eksenine bakarken kafanızı belirli bir derece döndürerek bunu gözünüzde canlandırmaya çalışın. Örneğin 3- boyutlu bir dünyada 2- boyutlu vektörleri döndürürken, dönüş eksenini z- eksenine ayarlıyoruz (bunu gözünüzde canlandırmaya çalışın).

Vektörleri trigonometri kullanarak bir açı verildiğinde yeni döndürülmüş vektörlere dönüştürmek mümkündür. Bu genellikle sineve cosine işlevlerinin (genellikle sinve cosolarak kısaltılır) akıllıca bir kombinasyonu ile yapılır. Döndürme matrislerinin nasıl üretildiğine dair bir tartışma bu bölümün kapsamı dışındadır.

Döndürme matrisi, açının $\theta$ sembolü olarak gösterildiği 3- boyutlu uzaydaki her birim ekseni için tanımlanır.

X-ekseni etrafında döndürme :

$$\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}{\cos \theta} & - \color{green}{\sin \theta} & \color{green}0 \\ \color{blue}0 & \color{blue}{\sin \theta} & \color{blue}{\cos \theta} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ \color{green}{\cos \theta} \cdot y - \color{green}{\sin \theta} \cdot z \\ \color{blue}{\sin \theta} \cdot y + \color{blue}{\cos \theta} \cdot z \\ 1 \end{pmatrix}$$

Y-ekseni etrafında döndürme :

$$\begin{bmatrix} \color{red}{\cos \theta} & \color{red}0 & \color{red}{\sin \theta} & \color{red}0 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}0 \\ - \color{blue}{\sin \theta} & \color{blue}0 & \color{blue}{\cos \theta} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{\cos \theta} \cdot x + \color{red}{\sin \theta} \cdot z \\ y \\ - \color{blue}{\sin \theta} \cdot x + \color{blue}{\cos \theta} \cdot z \\ 1 \end{pmatrix}$$

Z-ekseni etrafında döndürme :

$$\begin{bmatrix} \color{red}{\cos \theta} & - \color{red}{\sin \theta} & \color{red}0 & \color{red}0 \\ \color{green}{\sin \theta} & \color{green}{\cos \theta} & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{\cos \theta} \cdot x - \color{red}{\sin \theta} \cdot y \\ \color{green}{\sin \theta} \cdot x + \color{green}{\cos \theta} \cdot y \\ z \\ 1 \end{pmatrix}$$

Döndürme matrislerini kullanarak konum vektörlerimizi üç birim eksenden biri etrafında dönüştürebiliriz. Rasgele bir 3B eksen etrafında döndürmek için, önce X- ekseninin etrafında, sonra Y ve sonra Z'nin etrafında dönerek bunların hepsini birleştirebiliriz. Ancak, bu hızlı bir şekilde Gimbal Lock adı verilen bir sorunu ortaya çıkarır. Ayrıntıları tartışmayacağız, ancak daha iyi bir çözüm, döndürme matrislerini birleştirmek yerine rastgele bir birim eksen etrafında dönmektir; sözgelimi (0.662,0.2,0.722) (bunun bir birim vektör olduğuna dikkat edin). Böyle bir (ayrıntılı) matris vardır ve keyfi dönüş ekseni olarak $(\color{red}{R_x}, \color{green}{R_y}, \color{blue}{R_z})$ ile birlikte verilir:

$$\begin{bmatrix} \cos \theta + \color{red}{R_x}^2(1 - \cos \theta) & \color{red}{R_x}\color{green}{R_y}(1 - \cos \theta) - \color{blue}{R_z} \sin \theta & \color{red}{R_x}\color{blue}{R_z}(1 - \cos \theta) + \color{green}{R_y} \sin \theta & 0 \\ \color{green}{R_y}\color{red}{R_x} (1 - \cos \theta) + \color{blue}{R_z} \sin \theta & \cos \theta + \color{green}{R_y}^2(1 - \cos \theta) & \color{green}{R_y}\color{blue}{R_z}(1 - \cos \theta) - \color{red}{R_x} \sin \theta & 0 \\ \color{blue}{R_z}\color{red}{R_x}(1 - \cos \theta) - \color{green}{R_y} \sin \theta & \color{blue}{R_z}\color{green}{R_y}(1 - \cos \theta) + \color{red}{R_x} \sin \theta & \cos \theta + \color{blue}{R_z}^2(1 - \cos \theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

Böyle bir matris üretmenin matematiksel tartışması bu bölümün kapsamı dışındadır. Bu matrisin bile gimbal lock'u tamamen önleyemediğini unutmayın (çok daha zorlasa da). Gimbal lock'u gerçekten önlemek için, sadece daha güvenli değil, aynı zamanda daha hesaplama dostu olan dördeyleri (ing. quaternion) kullanarak döndürmeyi temsil etmeliyiz. Ancak, dördey tartışması da bu bölümün kapsamı dışındadır.

Matrisleri Birleştirme

Dönüşümler için matrisleri kullanmanın gerçek gücü, matris-matris çarpımı sayesinde çoklu dönüşümleri tek bir matriste birleştirebilmemizdir. Birkaç dönüşümü birleştiren bir dönüşüm matrisi üretip üretemeyeceğimizi görelim. Diyelim ki bir vektörünüz (x,y,z) var ve bunu 2 ile ölçeklendirmek ve sonra (1,2,3) ile ötelemek istiyoruz. Gerekli adımlarımız için bir öteleme ve ölçeklendirme matrisine ihtiyacımız var. Sonuçta elde edilen dönüşüm matrisi şöyle görünecektir:

$$Trans . Scale = \begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} . \begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix}$$

Matrisleri çarparken önce öteleme sonra ölçek dönüşümü yaptığımızı unutmayın. Matris çarpımı değişmeli değildir, yani sıraları önemlidir. Matrisleri çarparken, en sağdaki matris önce vektörle çarpılır, bu yüzden çarpımları sağdan sola okumalısınız. Matrisleri birleştirirken önce ölçekleme işlemlerinin, ardından dönüşlerin ve son olarak ötelemenin yapılması tavsiye edilir, aksi takdirde birbirlerini (olumsuz) etkileyebilirler. Örneğin, önce bir öteleme yapar ve sonra ölçeklendirirseniz, öteleme vektörü de ölçeklenir!

Son dönüşüm matrisini vektörümüz üzerinde çalıştırmak aşağıdaki vektör ile sonuçlanır:

$$\begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} . \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \color{red}2x + \color{red}1 \\ \color{green}2y + \color{green}2 \\ \color{blue}2z + \color{blue}3 \\ 1 \end{bmatrix}$$

Harika! Vektör önce iki ile ölçeklenir ve sonra (1,2,3) ile ötelenir.

Pratikte

Artık dönüşümlerin arkasındaki tüm teoriyi açıkladığımıza göre, bu bilgiyi gerçekten bizim lehimize nasıl kullanabileceğimizi görmenin zamanı geldi. OpenGL' de herhangi bir matris veya vektör bilgisi yerleşik değildir, bu nedenle kendi matematik sınıflarımızı ve fonksiyonlarımızı tanımlamamız gerekir. Bu eğitselde tüm küçük matematiksel detaylardan soyutlanmayı tercih ediyoruz ve sadece önceden hazırlanmış matematik kütüphanelerini kullanıyoruz. Neyse ki, GLM adı verilen kullanımı kolay ve uyarlanmış OpenGL matematik kütüphanesi var.

GLM

GLM , OpenGL Matematik' in kısaltmasıdır ve yalnızca üstbilgi (ing. header-only) kütüphanesidir, yani yalnızca uygun başlık dosyalarını eklememiz gerekir ve işimiz biter; hiçbir bağlantı kurma ve derleme işlemi gerekmez. GLM, kendi web sitesinden indirilebilir. Başlık dosyalarının kök dizinini includes klasörümüze kopyalarız ve ilerleriz.

İhtiyacımız olabilecek GLM işlevlerinin çoğu, aşağıdaki gibi ekleyeceğimiz 3 başlık dosyasında bulunmaktadır:

#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>

(1,0,0) vektörünü (1,1,0) çevirerek dönüşüm bilgimizi iyi bir şekilde kullanıp kullanamayacağımızı görelim (homojen koordinatı 1.0olarak ayarlanmış bir glm::vec4 olarak tanımladığımızı unutmayın):

glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
glm::mat4 trans = glm::mat4(1.0f);
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
std::cout << vec.x << vec.y << vec.z << std::endl;

İlk olarak GLM'nin içinde var olan vektör sınıfını kullanarak vecadında bir vektör tanımlarız. Daha sonramat4tipinde bir matris tanımlarız ve matrisin köşegenlerini 1.0' a ayarlayarak birim matrisine ilklendiririz; eğer bunu birim matrisine ilklendirmezsek, matris bir $null$ matris (tüm elemanları 0 ) olur ve sonraki tüm matris işlemleri de bir $null$ matrisle sonuçlanır.

Bir sonraki adım, birim matrisimizi glm::translate işlevine bir öteleme vektörü ile birlikte geçirerek bir dönüşüm matrisi oluşturmaktır (verilen matris daha sonra bir öteleme matrisi ile çarpılır ve elde edilen matris döndürülür).

Sonra vektörümüzü dönüşüm matrisi ile çarpar ve sonucu elde ederiz. Matris ötelemenin nasıl çalıştığını hâlâ hatırlıyorsak, elde edilen vektör (1+1,0+1,0+0) yani(2,1,0) olmalıdır. Bu kod parçası 210 çıktı, ve öteleme matrisi görevini yaptı.

Daha ilginç bir şey yapalım ve önceki bölümdeki konteyner nesnesini ölçeklendirelim ve döndürelim:

glm::mat4 trans = glm::mat4(1.0f);
trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));  

İlk önce konteyneri her eksende 0.5 ölçeklendirir ve ardından Z- ekseni etrafında 90 derece döndürürüz. GLM radyan cinsinden açıları kullanır, bu yüzden dereceleri glm::radians kullanarak radyanlara dönüştürürüz. Dokulu dikdörtgenin XY düzleminde olduğuna dikkat edin, işte bu yüzden Z- ekseni etrafında döndürmek istiyoruz. Döndürdüğümüz eksenin birim vektör olması gerektiğini unutmayın, bu nedenle X, Y veya Z- ekseni etrafında dönmüyorsanız önce vektörü normalleştirdiğinizden emin olun. Matrisi GLM işlevlerinin her birine geçirdiğimiz için, GLM matrisleri otomatik olarak birlikte çarparak tüm dönüşümleri birleştiren bir dönüşüm matrisi elde edilir.

Bir sonraki büyük soru: dönüşüm matrisini gölgelendiricilere nasıl ulaştıracağız? Daha önce kısaca bahsettik, GLSL' in bir mat4tipi de var. Böylece, köşe nokta gölgelendiricisini bir mat4üniform değişkenini alacak ve konum vektörünü uniform matris değeri ile çarpacağız:

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;

out vec2 TexCoord;
  
uniform mat4 transform;

void main()
{
    gl_Position = transform * vec4(aPos, 1.0f);
    TexCoord = vec2(aTexCoord.x, aTexCoord.y);
} 

GLSL ayrıca, vektörlerde benzerleri olduğu gibi mat2ve mat3tiplerine de sahiptir. Matris tiplerinde yukarıda belirtilen tüm matematik işlemlerine (skaler-matris çarpımı, matris-vektör çarpımı ve matris-matris çarpımı gibi) izin verilir. Özel matris operasyonlarının kullanıldığı yerde, neler olduğunu açıklayacağız.

uniform değeri ekledik ve gl_Position' a geçirmeden önce konum vektörünü dönüşüm matrisi ile çarptık. Konteynerimiz şimdi iki kat daha küçük ve 90derece döndürülmüş olmalıdır (sola yatık). Yine de dönüşüm matrisini gölgelendiriciye geçirmeliyiz:

unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));

Önce uniform değişkenin konumunu sorgularız ve daha sonra matris verisini son ek olarak Matrix4fvile glUniform kullanarak gölgelendiricilere göndeririz. İlk argüman uniform değerin konumu olduğundan tanıdık gelmelidir. İkinci argüman OpenGL' e kaç matris göndermek istediğimizi söyler, bu da 1'dir. Üçüncü argüman bize matrisimizi değiştirmek isteyip istemediğimizi, yani sütunları ve satırları değiştirmek isteyip istemediğinizi sorar. OpenGL geliştiricileri genellikle GLM' deki varsayılan matris düzeni olan sütun- majör sıralama adı verilen dahili bir matris düzeni kullanırlar, bu nedenle matrisleri aktarmaya gerek yoktur; yani GL_FALSE konumunda tutabiliriz. Son parametre gerçek matris verisidir, ancak GLM matrislerinin verilerini her zaman OpenGL' in beklentilerine uymayacak şekilde saklar, bu yüzden verileri önce GLM' in kendi içinde yer alan value_ptr işlevi ile dönüştürürüz.

Bir dönüşüm matrisi oluşturduk, köşe nokta gölgelendiricisinde uniform değişken bildirimi yaptık ve matrisi, köşe nokta koordinatlarımızı dönüştürdüğümüz gölgelendiricilere gönderdik. Sonuç şöyle görünmelidir:

Mükemmel! Konteynerimiz gerçekten sola yatık ve iki kat daha küçük olduğundan dönüşüm başarılı oldu. Biraz daha ürkek olalım ve konteyneri zaman içinde döndürüp döndüremeyeceğimize bir bakalım ve eğlenmek için konteyneri pencerenin sağ alt tarafına yeniden konumlandıralım. Konteyneri zaman içinde döndürmek için sahneleme döngüsünde dönüşüm matrisini güncellemeliyiz çünkü her kareyi güncellemesi gerekir. Zaman içinde bir açı elde etmek için GLFW' nin zaman fonksiyonunu kullanıyoruz:

glm::mat4 trans = glm::mat4(1.0f);
trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f));
trans = glm::rotate(trans, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));

Önceki durumda, dönüşüm matrisini herhangi bir yerde beyan edebileceğimizi unutmayın, ancak şimdi dönüşü sürekli güncellemek için her yinelemeyi oluşturmanız gerekiyor. Bu, sahneleme döngüsünün her yinelemesinde dönüşüm matrisini yeniden yaratmamız gerektiği anlamına gelir. Genellikle sahneleri oluştururken, her karede yeni değerlerle yeniden oluşturulan birkaç dönüşüm matrisimiz bulunur.

Burada konteyneri önce orijin noktası (0,0,0) etrafında döndürüyoruz ve sonra, döndürülmüş halini ekranın sağ alt köşesine öteliyoruz. Gerçek dönüşüm sırasının tersine okunması gerektiğini unutmayın: kodda ilk önce çevirip sonra döndürüyor olsak da, gerçek dönüşümler önce bir dönüş ve sonra bir öteleme uygular. Tüm bu dönüşüm kombinasyonlarını ve bunların nesnelere nasıl uygulandığını anlamak zordur. Bu tip dönüşümleri deneyin ve hızlı bir şekilde kavrayın.

Bu adımları doğru yaptıysanız, aşağıda ekli bulunan video dosyasında görebileceğiniz sonucu elde etmelisiniz:

3MB

LearnOpenGL - Transformations.mp4

Ve işte buyurun. Zaman içinde döndürülen, tümü tek bir dönüşüm matrisi tarafından yapılan ötelenmiş bir konteyner! Şimdi matrislerin neden grafik alanında bu kadar güçlü bir yapı olduğunu anlayabilirsiniz. Sonsuz miktarda dönüşüm tanımlayabilir ve hepsini istediğimiz sıklıkta tekrar kullanabileceğimiz tek bir matriste birleştirebiliriz. Köşe noktası gölgelendiricisinde böyle dönüşümleri kullanmak, köşe nokta verisini yeniden tanımlama çabasından kurtarır ve verilerimizi her zaman yeniden göndermek zorunda olmadığımızdan (çünkü bu oldukça yavaştır) bize de biraz işlem süresi kazandırır; tek yapmamız gereken uniform dönüşüm değişkenini güncellemektir.

Doğru sonucu elde edemediyseniz veya başka bir yere takıldıysanız, kaynak koda ve güncellenmiş gölgelendirici sınıfına bakın.

Bir sonraki bölümde, köşe noktalarımız için farklı koordinat alanları tanımlama amacıyla matrisleri nasıl kullanabileceğimizi tartışacağız. Bu, 3- boyutlu grafiklere ilk adımımız olacak.

İlave Okuma

• Lineer Cebirin Özü: Dönüşümler ve lineer cebirin altında yatan matematiği açıklayan harika video eğitim serisi, Grant Sanderson tarafından sunulmuştur.

Alıştırmalar

• Konteynerdeki son dönüşümü kullanarak, onu önce döndürüp sonra öteleyerek değiştirmeyi deneyin. Ne olduğunu görün ve bunun neden olduğunu anlamaya çalışın: çözüm.

• Başka bir glDrawElements çağrısıyla ikinci bir konteyner çizmeyi deneyin, ama yalnızca dönüşümleri kullanarak farklı bir konuma yerleştirin. Bu ikinci konteynerin çizim penceresinin sol üst köşesine yerleştirildiğinden emin olun ve döndürmek yerine zaman içinde ölçeklendirin (burada sin

  işlevini kullanmak yararlıdır; sinkullanınca nesnenin negatif bir ölçek olur olmaz tersine çevrileceğini unutmayın): çözüm

Orijinal Kaynak: Transformations

Çeviri: Nezihe Sözen