Koordinat Sistemleri

Son bölümde, tüm köşe noktalarını dönüşüm matrisleri ile dönüştürerek matrisleri nasıl faydalı kullanabileceğimizi öğrendik. OpenGL, görünür olmasını istediğimiz tüm köşe noktalarının, her köşe nokta gölgelendirici çalışmasından sonra normalleştirilmiş aygıt koordinatlarında olmasını bekler. Yani, her bir köşe noktasının x, yve zkoordinatları -1.0 ile 1.0arasında olmalıdır; bu aralığın dışındaki koordinatlar görünmez. Genellikle yaptığımız şey, kendi belirlediğimiz bir aralıktaki (veya uzaydaki) koordinatları belirtmektir ve köşe nokta gölgelendirici de bu koordinatları normalleştirilmiş aygıt koordinatlarına (NDC) dönüştürür. Bu normalleştirilmiş koordinatlar daha sonra ekranınızdaki 2-boyutlu koordinatlara yani piksele dönüştürülmek üzere pikselleştiriciye (ing. rasterizer) verilir.

Koordinatları NDC'ye dönüştürmek adım adım gerçekleştirilir ve bu adımlarda genellikle bir nesnenin köşe noktalarını birkaç koordinat sistemine dönüştürmek gerekir. Köşe noktalarını birkaç ara koordinat sistemine dönüştürmenin avantajı, belli koordinat sistemlerinde bazı hesaplamaların daha kolay olmasıdır. Bizim için önemli olan toplam 5 farklı koordinat sistemi vardır:

Yerel uzay (ya da Nesne uzayı)
Dünya Uzayı
Görünüm uzayı (ya da Göz Uzayı)
Kırpma uzayı
Ekran uzayı

Bunların hepsi, sonunda parçalara ayrılmadan önce köşe noktalarımızın dönüştürüleceği farklı bir durumdur.

Muhtemelen bir uzay ya da koordinat sisteminin aslında ne olduğu konusunda oldukça şaşkınsınız, bu yüzden önce resmin bütününü ve her bir özel alanın neyi temsil ettiğini daha anlaşılır bir şekilde açıklayalım.

Büyük resim

Koordinatları bir uzaydan başka bir koordinat uzayına dönüştürmek için en önemlileri model, görünüm ve projeksiyon matrisi olan birkaç dönüşüm matrisini kullanacağız. Köşe nokta koordinatlarımız önce yerel uzayda yerel koordinatlar olarak başlar ve daha sonra dünya koordinatlarına, görünüm koordinatlarına, kırpma koordinatlarına işlenir ve ekran koordinatları olarak son bulur. Aşağıdaki görsel işlem basamaklarını ifade etmektedir ve her dönüşümün ne yaptığını gösterir:

Yerel koordinatlar, nesnenizin yerel orijinine göre olan koordinatlarıdır; yani nesnenizin başladığı koordinatlardır.
Bir sonraki adım, yerel koordinatları daha büyük bir dünya için dünya-uzayı koordinatlarına dönüştürmektir. Bu koordinatlar, dünyanın orijinine göre yerleştirilmiş diğer birçok nesne ile birlikte
küresel orijinlerine göredir.
Daha sonra dünya koordinatlarını, her bir koordinat kameradan veya izleyicinin bakış açısından görülebilecek şekilde görünüm uzayı koordinatlarına dönüştürüyoruz.
Koordinatlar görünüm uzayı içinde olduktan sonra, koordinatları kırpmak üzere onların iz düşümünü almak (ing. project) istiyoruz. Kırpma koordinatları -1.0ve 1.0aralığına işlenir ve ekranda hangi köşe noktalarının sonlanacağını belirler. Kırpma uzayı koordinatlarına, perspektif projeksiyonu kullanılıyorsa perspektif de eklenebilir.
Son olarak, koordinatları -1.0ve 1.0'dan glViewport ile tanımlanan koordinat aralığına dönüştüren görüş alanı dönüşümü dediğimiz bir işlem aracılığıyla kırpma koordinatlarını ekran koordinatlarına dönüştürüyoruz. Elde edilen koordinatlar daha sonra parçalara dönüştürülmek üzere pikselleştiriciye gönderilir.

Muhtemelen her bir uzayın ne için kullanıldığına dair küçük bir fikriniz oluştu. Köşe noktalarımızı tüm bu farklı uzaylara dönüştürmemizin nedeni, bazı işlemlerin belirli koordinat sistemlerinde daha anlamlı veya daha kolay kullanılmasıdır. Örneğin, nesnenizi değiştirirken bunu yerel alanda yapmak en mantıklıdır, diğer nesnelerin konumuna göre nesne üzerinde belirli işlemleri hesaplarken dünya koordinatlarında yapmak gibi... İstersek, yerel uzaydan tek seferde uzayı kırpmaya giden bir dönüşüm matrisi tanımlayabiliriz, ancak bu bizi daha az esneklikle bırakır.

Her bir koordinat sistemini aşağıda daha ayrıntılı olarak ele alacağız.

Yerel Uzay (ing. Local space)

Yerel uzay, nesneniz için yerel olan, yani nesnenizin başladığı koordinat uzayıdır. Küpünüzü bir modelleme yazılım programında (Blender gibi) oluşturduğunuzu düşünün. Küpünüzü son uygulamanızda farklı bir konumda bırakmanıza rağmen, küpünüzün orijini muhtemelen (0,0,0)' dır. Muhtemelen, oluşturduğunuz tüm modellerin başlangıç pozisyonları (0,0,0) 'dır. Bu nedenle modelinizin tüm köşeleri yerel alandadır: hepsi nesneniz için yereldir.

Kullandığımız konteynerin köşe noktaları, başlangıç noktası olarak 0.0 ile -0.5 ve 0.5 arasında koordinatlar olarak belirtildi. Bunlar yerel koordinatlardır.

Dünya uzayı (ing. World space)

Tüm nesnelerimizi doğrudan uygulama içine aldığımızda, muhtemelen dünyanın (0,0,0) orijininde birbirlerinin içine yerleştirilmiş bir yer olurdu ki bu bizim istediğimiz bir durum değildir. Her bir nesne özelinde onları daha büyük bir dünyanın içine yerleştirmek için bir konum tanımlamak istiyoruz. Dünya uzayındaki koordinatlar tam olarak göründükleri gibidir: (oyun) dünyasına göre tüm köşelerinizin koordinatlarıdır. Bu, nesnelerinizin yerin etrafına (tercihen gerçekçi bir şekilde) dağılmış şekilde dönüştürülmesini istediğiniz koordinat uzayıdır. Nesnenin koordinatları yerelden dünya uzayına dönüştürülür. Bu işlem model matrisi ile gerçekleştirilir.

Model matrisi, nesnenizi dünyaya ait olduğu bir yerde/ yönde yerleştirmek için öteleyen, ölçeklendiren ve döndüren bir dönüşüm matrisidir.Bir evi ölçeklendirerek (çünkü yerel uzay için biraz fazla büyük), bir banliyö kasabasına öteleyerek ve y-ekseninde biraz sola döndürerek onu komşu evlere düzgün bir şekilde sığacak şekilde dönüştürdüğünüzü düşünün. Konteyneri sahnenin her yerine bir tür model matrisi olarak konumlandırmak için önceki bölümdeki matrisi düşünebilirsiniz. Konteynerin yerel koordinatlarını sahnede/ dünyada farklı bir konuma dönüştürdük.

Görünüm uzayı (ing. View space)

Görünüm uzayı, insanların genellikle OpenGL' in kamerası olarak adlandırdığı şeydir (bazen kamera uzayı veya göz uzayı olarak da bilinir). Görünüm uzayı, dünya uzay koordinatlarınızı kullanıcının baktığı koordinatlara dönüştürmenin sonucudur. Dolayısıyla görünüm uzayı, kameranın bakış açısından görüldüğü gibidir. Bu genellikle sahneyi ötelemek/döndürmek için ötelemelerinve döndürmelerin bir birleşimi olarak gerçekleştirilir. Böylece belirli öğeler kameranın ön kısmına gelecek şekilde dönüştürülür. Bu birleşik dönüşümler genellikle dünya koordinatlarını görünüm uzayına dönüştüren bir görünüm matrisinin içinde saklanır. Bir sonraki bölümde, bir kamerayı simüle etmek için böyle bir görünüm matrisinin nasıl oluşturulacağını kapsamlı bir şekilde tartışacağız.

Kırpma uzayı (ing. Clip space)

Her köşe nokta gölgelendirici çalıştırılmasının sonunda OpenGL, koordinatların belirli bir aralıkta olmasını bekler ve bu aralığın dışında kalan tüm koordinatlar kırpılır. Kırpılan koordinatlar atılır, böylece kalan koordinatlar ekranınızda görünen parçalar olarak sonuçlanır. Burası aynı zamanda kırpma uzayının adını aldığı yerdir.

Görünür tüm koordinatları -1.0 ve 1.0 aralığında belirtmek gerçekten işlevsel olmadığından, çalışmak için kendi koordinat setimizi belirleriz ve OpenGL' in beklediği gibi bunları NDC'ye dönüştürürüz.

Tepe nokta koordinatlarını görünüm uzayından kırpma uzayına dönüştürmek için, bir koordinat aralığı belirten projeksiyon matrisi (ör. her boyut için -1000 ve 1000) tanımlanır. Projeksiyon matrisi daha sonra bu belirtilen aralıktaki koordinatları normalleştirilmiş aygıt koordinatlarına (-1.0, 1.0) dönüştürür. Bu aralığın dışındaki tüm koordinatlar -1.0 ile1.0arasında eşleştirilemediği için kırpılır. Projeksiyon matrisinde belirttiğimiz bu aralık ile (1250, 500, 750) koordinatı görünmez, çünkü x-koordinatı aralık dışındadır ve NDC'de 1.0'dan daha yüksek bir koordinata dönüştürülür, bu nedenle de kırpılır.

Bir ilkelin (sözgelimi üçgen olsun) yalnızca bir kısmı kırpma hacminin dışındaysa OpenGL' in bu ilkeli kırpma aralığına sığacak şekilde bir veya daha fazla üçgen olarak yeniden yapılandıracağını unutmayın.

Bir projeksiyon matrisinin oluşturduğu bu görüntüleme kutusuna frustum denir ve bu frustumun içinde kalan her koordinat kullanıcının ekranında sona erer. Belirli bir aralıktaki koordinatları 2B görünüm uzayı koordinatlarına kolayca eşleştirilebilen NDC'ye dönüştürme işlemine projeksiyon denir çünkü projeksiyon matrisi 3B koordinatları eşlemesi kolay 2B normalleştirilmiş aygıt koordinatlarına iz düşürür.

Bütün köşe noktaları kırpma uzayına dönüştürüldükten sonra, konum vektörlerinin x, y vezbileşenlerini vektörün homojen w bileşenine böldüğümüz perspektif bölünümü adı verilen son bir işlem gerçekleştirilir; perspektif bölünümü, 4B kırpma alanı koordinatlarını 3B normalleştirilmiş aygıt koordinatlarına dönüştüren şeydir. Bu adım, köşe nokta gölgelendirici adımının sonunda otomatik olarak gerçekleştirilir.

Bu aşamadan sonra ortaya çıkan koordinatlar ekran koordinatları ile (glViewport kullanarak) eşleştirilir ve parçalara (ing. fragment) dönüştürülür.

Görünüm koordinatlarını kırpma koordinatlarına dönüştürmek için kullanılan projeksiyon matrisi genellikle her formun kendine özgü frustum tanımladığı iki farklı biçim alır. Ortografik bir projeksiyon matrisi veya bir perspektif projeksiyon matrisi oluşturabiliriz.

Ortografik izdüşüm

Ortografik bir projeksiyon matrisi, bu kutunun dışındaki her bir köşe noktasının kırpıldığı kırpma uzayını tanımlayan küp benzeri bir frustum kutusunu tanımlar. Ortografik bir projeksiyon matrisi oluştururken görünür frustumun genişliğini, yüksekliğini ve uzunluğunu belirtiriz. Bu frustum içindeki tüm koordinatlar, matris tarafından dönüştürüldükten sonra NDC aralığı içinde sona erecek ve bu nedenle kırpılmayacaktır. Frustum biraz da bir konteynere benziyor:

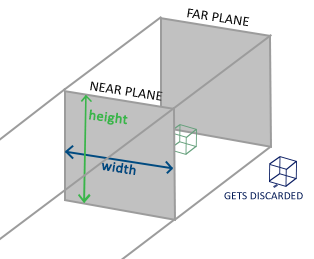
Frustum görünebilir koordinatlar tanımlar ve bir genişlik, bir yükseklik ve yakın ve uzak bir düzlemle belirtilir. Yakın düzlemin önündeki herhangi bir koordinat kırpılır ve aynısı uzak düzlemin arkasındaki koordinatlar için de geçerlidir. Ortografik frustum, dönüştürülmüş vektörün w bileşenine dokunamayacağı için, frustum içindeki tüm koordinatları özel bir yan etki olmadan normalleştirilmiş aygıt koordinatlarına doğrudan eşler; w bileşeni 1.0'a eşit kalırsa perspektif bölünümü koordinatları değiştirmez.

Ortografik bir projeksiyon matrisi oluşturmak için GLM' in kendi içinde bulunan işlevi glm::ortho 'yu kullanıyoruz:

glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);

İlk iki parametre frustumun sol ve sağ koordinatını, üçüncü ve dördüncü parametre frustumun alt ve üst kısmını belirtir. Bu 4 nokta ile yakın ve uzak düzlemlerin boyutunu; 5. ve 6. parametreler ile yakın ve uzak düzlem arasındaki mesafeleri tanımladık. Bu özel izdüşüm matrisi, x, y vez aralığı değerleri arasındaki tüm koordinatları normalleştirilmiş aygıt koordinatlarına dönüştürür.

Ortografik bir izdüşüm matrisi, koordinatları doğrudan ekranınız olan 2-boyutlu düzlemle eşleştirir, ancak gerçekte doğrudan bir izdüşüm, izdüşüm perspektifi dikkate almadığı için gerçekçi olmayan sonuçlar üretir. Bu, perspektif izdüşüm matrisinin bizim için düzelttiği şeydir.

Perspektif izdüşüm

Eğer gerçek hayatın sunduğu grafiklerden hoşlanıyorsanız, daha uzaktaki nesnelerin çok daha küçük göründüğünü fark edeceksiniz. Bu garip etki, perspektif dediğimiz şeydir. Perspektif, özellikle aşağıdaki görselde görüldüğü gibi sonsuz bir otoyolun veya demiryolunun ucuna bakıldığında fark edilir:

Gördüğünüz gibi, perspektif nedeniyle çizgiler yeterince uzak bir mesafede kesişiyor. Bu tam olarak perspektif izdüşümünün taklit etmeye çalıştığı etkidir ve bunu bir perspektif izdüşüm matrisi kullanarak yapar. İzdüşüm matrisi, belirli bir frustum aralığını kırpma uzayına eşler, ancak her bir köşe nokta koordinatının w değerini, bir köşe nokta koordinatı görüntüleyiciden ne kadar uzakta olursa, bu w bileşeni o kadar yüksek olacak şekilde manipüle eder. Koordinatlar kırpma uzayına dönüştürüldükten sonra -wila w aralığındadır (bu aralığın dışındaki herhangi bir şey kırpılacatır). OpenGL, görünür köşe nokta koordinatlarının son köşe nokta gölgelendirici çıktısı olarak -1.0 ve1.0 arasında olmasını gerektirir, bu nedenle koordinatlar kırpma uzayında olduğunda, perspektif bölünümü kırpma uzayı koordinatlarına uygulanır:

out = \begin{pmatrix} x /w \\ y / w \\ z / w \end{pmatrix}

Köşe nokta koordinatının her bir bileşeni, bir izleyiciden ne kadar uzakta olursa, küçük köşe koordinatlarını veren w bileşenine bölünür. Bu w bileşeni önemlidir, çünkü perspektif izdüşümünde bize yardımcı olur. Sonuçta elde edilen koordinatlar normalleştirilmiş aygıt uzayındadır. Ortografik ve perspektif izdüşüm matrislerinin gerçekte nasıl hesaplandığını öğrenmek istiyorsanız (ve matematikten de çok korkmuyorsanız) Songho' nun bu mükemmel makalesini önerebilirim.

Bir perspektif izdüşüm matrisi GLM' de aşağıdaki gibi oluşturulabilir:

glm::mat4 proj = glm::perspective(glm::radians(45.0f), (float)width/(float)height, 0.1f, 100.0f);

glm::perspective'in yaptığı, görünür uzayı tanımlayan büyük bir frustum yaratmaktır, frustum dışındaki herhangi bir şey kırpma uzayı hacmine girmeyecek ve böylece kırpılacaktır. Bir perspektif frustum, bu kutunun içindeki her koordinatın kırpma uzayındaki bir noktaya eşleştirileceği düzgün olmayan şekilli bir kutu olarak görselleştirilebilir. Perspektif bir frustumun görüntüsü aşağıda gibidir:

İlk parametresi, görünüm uzayını temsil eden ve görüş alanının (ing. field of view) ne kadar büyük olacağını belirleyen fov değerini belirtir. Gerçekçi bir görünüm için genellikle 45 dereceye ayarlanır, ancak Doom-tarzı sonuçlar elde etmek için daha yüksek bir değere ayarlayabilirsiniz. İkinci parametre, görüş alanının (ing. viewport) genişliğinin yüksekliğine bölünmesiyle hesaplanan en boy oranını ayarlar. Üçüncü ve dördüncü parametre, frustumun yakın ve uzak düzlemini ayarlar. Genellikle yakın mesafeyi 0.1'e ve uzak mesafeyi 100.0'a ayarladız. Yakın ve uzak düzlem arasındaki ve frustum içindeki tüm köşe noktaları sahnelenecektir.

Perspektif matrisinizin yakın değeri çok yüksek ayarlandığında (10.0gibi), OpenGL kameraya yakın olan tüm koordinatları (0.0 ve10.0arasında) kırpar, bu da video oyunlarında daha önce görmüş olabileceğiniz rahatsız edici bir görsel bir sonuç verebilir.

Ortografik izdüşüm kullanıldığında, köşe nokta koordinatlarının her biri herhangi bir perspektif bölünümü olmadan kırpma uzayına doğrudan eşleştirilir (yine de perspektif bölünümü yapılır, ancak wbileşeni manipüle edilmez,1 olarak kalır ve bu nedenle etkisi yoktur). Ortografik izdüşümde, perspektif izdüşümü kullanmadığından, uzaktaki nesneler daha küçük görünmez, bu da garip bir görsel çıktı üretir. Bu nedenle ortografik izdüşüm esas olarak 2B sahneleme ve perspektifle çarpık köşeleri istemediğimiz bazı mimari veya mühendislik uygulamaları için kullanılır. 3B modelleme için kullanılan Blender gibi uygulamalar bazen modelleme için ortografik projeksiyon kullanır, çünkü her nesnenin boyutlarını daha doğru bir şekilde gösterir. Aşağıda Blender'daki her iki projeksiyon yönteminin bir karşılaştırmasını göreceksiniz:

Perspektif izdüşümde, daha uzaktaki köşe noktalarının çok daha küçük göründüğünü, ortografik izdüşümde ise her köşe noktasının kullanıcıyla aynı mesafeye sahip olduğunu görebilirsiniz.

Hepsini bir araya getirince

Yukarıda belirtilen adımların her biri için bir dönüşüm matrisi oluşturuyoruz: model, görünüm ve izdüşüm matrisi. Bir köşe noktası koordinatı, aşağıdaki yöntem ile kırpma koordinatlarına dönüştürülür:

V_{clip} = M_{projection} \cdot M_{view} \cdot M_{model} \cdot V_{local}

Matris çarpım sırasının tersten olduğunu unutmayın (matris çarpımını sağdan sola okumamız gerekir). Sonuçta elde edilen köşe noktası, köşe nokta gölgelendiricisinde gl_Position öğesine atanmalıdır ve OpenGL otomatik olarak perspektif bölünümü ve kırpma gerçekleştirecektir.

Ya sonra? Köşe nokta gölgelendiricisinin çıktısı, koordinatların dönüşüm matrisleri ile yaptığımız kırpma uzayında olmasını gerektirir. OpenGL daha sonra bunları normalleştirilmiş aygıt koordinatlarına dönüştürmek için kırpma-uzayı koordinatlarında perspektif bölünümü gerçekleştirir. Ardından normalleştirilmiş aygıt koordinatlarını, her koordinatın ekrandaki bir noktaya (bizim durumumuzda 800x600 ekran) karşılık geldiği ekran koordinatlarına eşlemek için glViewPort parametrelerini kullanır. Bu işleme görünüm alan dönüşümü (ing. viewport transform) denir.

Bu, anlaşılması zor bir konu. Bu nedenle her bir uzayın ne için kullanıldığından hâlâ emin değilseniz endişelenmenize gerek yok. Aşağıda bu koordinat uzaylarını nasıl iyi bir şekilde kullanabileceğimizi göreceksiniz ve gelecek bölümlerde yeterince örnek olacak.

Üçüncü boyuta gidiyoruz

Artık 3-boyutlu koordinatların 2-boyutlu koordinatlara nasıl dönüştürüleceğini bildiğimize göre, şimdiye kadar gösterdiğimiz 2-boyutlu düzlem yerine gerçek 3-boyutlu nesneler oluşturmaya başlayabiliriz.

3-boyutlu çizim yapmaya başlamak için önce bir model matrisi oluşturacağız. Model matrisi, tüm nesnenin köşe noktalarını küresel dünya uzayına dönüştürmek için uygulamak istediğimiz öteleme, ölçeklendirme ve döndürmelerden oluşur. Düzlemimizi x-ekseni üzerinde döndürerek biraz değiştirelim, böylece yerdeymiş gibi görünüyor. Model matrisi daha sonra şöyle ifade edilecek:

glm::mat4 model = glm::mat4(1.0f);
model = glm::rotate(model, glm::radians(-55.0f), glm::vec3(1.0f, 0.0f, 0.0f));

Köşe nokta koordinatlarını bu model matrisi ile çarparak köşe nokta koordinatlarını, dünya koordinatlarına dönüştürüyoruz. Biraz zeminde olan düzlemimiz böylece küresel dünyadaki düzlemi temsil eder.

Ardından bir görünüm matrisi oluşturmamız gerekiyor. Nesnenin görünür hale gelmesi için sahnede biraz geriye doğru hareket etmek istiyoruz (dünya uzayında orijibi noktasındayız yani (0,0,0)). Sahnede dolaşmak için aşağıdakileri düşünün:

Bir kamerayı geriye doğru taşımak, tüm sahneyi ileriye taşımakla aynı şeydir.

Bir görünüm matrisinin yaptığı da tam olarak budur. Tüm sahneyi kameranın hareket etmesini istediğimiz yere ters çevirerek taşırız.

Çünkü geriye doğru hareket etmek istiyoruz ve OpenGL sağ el koordinat sistemini kullandığından pozitif z- ekseninde hareket etmeliyiz. Bunu sahneyi negatif z- eksenine çevirerek yapıyoruz. Yapılan şey geriye doğru hareket ettiğimiz izlenimini verecektir.

Sağ el koordinat sistemi

Geleneksel olarak, OpenGL sağ el koordinat sistemini kullanır. Bunun temel olarak söylediği şey, pozitif x-ekseninin sağa, pozitif y-ekseninin yukarı ve pozitif z-ekseninin geriye doğru olmasıdır. Ekranınızın 3 eksenin merkezi olduğunu ve ekranınızdan size doğru olan pozitif z-ekseninin olduğunu düşünün. Eksenler aşağıdaki gibi çizilir:

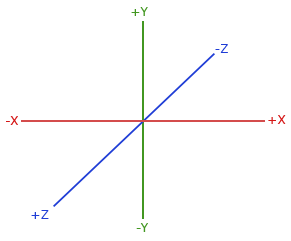
Neden sağ el koordinat sistemi olarak adlandırıldığını anlamak için aşağıdakileri yapın:

Sağ kolunuzu, eliniz yukarı gelecek şekilde pozitif y-ekseni boyunca uzatın.
Başparmağınız sağ tarafa baksın.
İşaret parmağınız yukarı baksın.
Şimdi orta parmağınızı 90 derece aşağı doğru bükün.

Aşamaları doğru yaptıysanız, baş parmağınız pozitif x- eksenine, işaret parmağı pozitif y- eksenine ve orta parmağınız pozitif z- eksenine doğru bakmalıdır. Bunu sol kolunuzla yapsaydınız z- ekseninin ters döndüğünü görürdünüz. Bu, sol el koordinat sistemi olarak bilinir ve DirectX tarafından yaygın olarak kullanılır. Normalleştirilmiş aygıt koordinatlarında OpenGL' in gerçekte sol el koordinat sistemi kullandığını (izdüşüm matrisi bu el koordinat sistemi değişimini sağlıyor) unutmayın.

Bir sonraki bölümde sahnede nasıl daha fazla hareket edileceğini tartışacağız. Şimdilik görünüm matrisi aşağıdaki gibidir:

glm::mat4 view = glm::mat4(1.0f);
// note that we're translating the scene in the reverse direction of where we want to move
view = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f));

Tanımlamamız gereken son şey izdüşüm matrisidir. Sahne için perspektif izdüşümü kullanmak istiyoruz, bu yüzden projeksiyon matrisini şöyle ifade edelim:

glm::mat4 projection;
projection = glm::perspective(glm::radians(45.0f), 800.0f / 600.0f, 0.1f, 100.0f);

Şimdi dönüşüm matrislerini yarattığımıza göre, bunları gölgelendiricilerimize geçirmeliyiz. İlk önce, dönüşüm matrislerini köşe nokta gölgelendiricisinde uniform olarak ifade edelim ve köşe nokta koordinatlarıyla çarpalım:

#version 330 core
layout (location = 0) in vec3 aPos;
...
uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;

void main()
{
    // note that we read the multiplication from right to left
    gl_Position = projection * view * model * vec4(aPos, 1.0);
    ...
}

Matrisleri gölgelendiriciye de göndermeliyiz (bu genellikle her bir çerçeve başına yapılır, çünkü dönüşüm matrisleri sürekli değişme eğilimindedir):

int modelLoc = glGetUniformLocation(ourShader.ID, "model");
glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
... // same for View Matrix and Projection Matrix

Artık köşe nokta koordinatlarımız model, görünüm ve izdüşüm matrisi ile dönüştürüldüğüne göre, son nesne şöyle olmalıdır:

Zemine doğru ters eğik.
Bizden bir parça uzakta.
Perspektif görünümdedir (yani köşe noktaları ne kadar uzakta ise o kadar küçük görünmeli).

Sonucun gerçekten bu özellikleri karşılayıp karşılamadığını kontrol edelim:

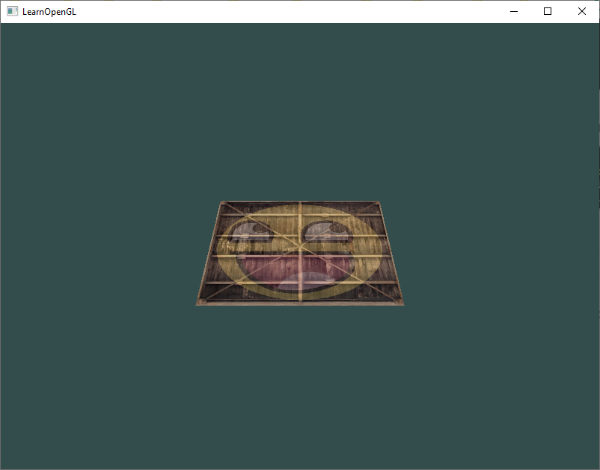
Gerçekten de hayali bir yerde duran 3-boyutlu bir düzlem gibi görünüyor. Aynı sonucu alamıyorsanız, kodunuzu tam kaynak koduyla karşılaştırın.

Daha fazla üçüncü boyut

Şimdiye kadar, 3B uzayda bile 2B düzlemde çalıştık, bu yüzden maceraya atılalım ve 2B düzlemimizi 3B bir küpe genişletelim. Bir küp oluşturmak için toplam 36 köşe noktasına ihtiyacımız var (6 yüz *2 üçgen * 3 köşe noktası). 36 köşe noktası özet geçilmesi gerekecek kadar fazladır, bu yüzden buradan alıp kullanabilirsiniz.

Eğlenmek için, küpün zamanla birlikte dönmesini sağlayacağız:

model = glm::rotate(model, (float)glfwGetTime() * glm::radians(50.0f), glm::vec3(0.5f, 1.0f, 0.0f));

Ve sonra küpü glDrawArrays kullanarak çizeceğiz (indisleri belirtmediğimiz gibi), ancak bu sefer 36 köşe noktasıyla...

glDrawArrays(GL_TRIANGLES, 0, 36);

Aşağıda ekli bulunan videodakine benzer bir şey görmelisiniz:

Bir küpü biraz andırıyor ama bir şeyler daha olmalı sanki. Küplerin bazı kenarları küpün diğer kenarlarına çiziliyor. Bunun nedeni, OpenGL küpünüzü üçgen- üçgen, parça- parça çizdiğinde, daha önce çizilmiş olabilecek piksel renklerinin üzerine yazdığındandır. OpenGL, aynı çizim çağrısında oluşturulan üçgenlerin sırası konusunda hiçbir garanti vermediğinden, biri açıkça birbirinin önünde olması gerekse bile bazı üçgenler üst üste çizilir.

Neyse ki OpenGL, derinlik bilgilerini, OpenGL' in ne zaman bir pikselin çizileceğini ve ne zaman yapılmayacağına karar vermesini sağlayan z-tamponu adlı bir arabellek barındırır. Z-tamponu kullanarak OpenGL' i derinlik testi yapacak şekilde yapılandırabiliriz.

Z-tamponu

OpenGL, tüm derinlik bilgilerini derinlik arabelleği olarak da bilinen bir z-tamponunda saklar. GLFW sizin için otomatik olarak böyle bir arabellek oluşturur (tıpkı çıkış imgesinin renklerini saklayan bir renk arabelleğine sahip olduğu gibi). Derinlik her bir parçanın içinde (parçanın z-değeri olarak) saklanır ve parçanın rengini çıktısını almak istediğinde, OpenGL derinlik değerlerini z-buffer ile karşılaştırır. Geçerli parça diğer parçanın arkasındaysa atılır, aksi takdirde üzerine yazılır. Bu işleme derinlik testi denir ve OpenGL tarafından otomatik olarak yapılır.

Ancak, OpenGL' in gerçekten derinlik testi yaptığından emin olmak istiyorsak, öncelikle OpenGL' e derinlik testini etkinleştirmek istediğimizi söylememiz gerekir; çünkü, varsayılan olarak devre dışıdır. glEnable kullanarak derinlik testini etkinleştirebiliriz. glEnable ve glDisable işlevleri, OpenGL' deki belirli işlevleri etkinleştirmemize ve devre dışı bırakmamıza olanak tanır. Bu işlev daha sonra devre dışı bırakmak ve etkinleştirmek için başka bir çağrı yapılana kadar durumunu korur. Şu anda GL_DEPTH_TEST özelliğini aktifleştirerek derinlik testini etkinleştirmek istediğimizi belirtiyoruz:

glEnable(GL_DEPTH_TEST);

Bir derinlik arabelleği kullandığımızda, her sahneleme yinelemesinden önce derinlik arabelleğini temizlemek istiyoruz (aksi takdirde önceki çerçevenin derinlik bilgisi arabellekte kalacaktır). Renk arabelleğini temizlemekte olduğu gibi, glClear işlevinde DEPTH_BUFFER_BIT bitini belirterek derinlik arabelleğini temizleyebiliriz:

glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

Programımızı yeniden çalıştıralım ve şimdi OpenGL' in derinlik testi yapıp yapmadığını görelim:

Vardık sayılır! Zaman ilerledikçe dönen, uygun derinlik testine sahip tamamen dokulu bir küp elde ettik. Kaynak kodu buradan kontrol edin.

Daha fazla küp!

Diyelim ki 10 küpü ekranda göstermek istiyoruz. Her küp aynı görünecek, ancak her biri farklı bir dönme ile dünyanın farklı bir yerinde olacaktır. Küpün grafik düzeni zaten tanımlanmıştı, bu nedenle daha fazla nesne oluştururken arabelleklerimizi veya öznitelik dizilerimizi değiştirmek zorunda değiliz. Her nesne için değiştirmemiz gereken tek şey, küpleri dünya içinde dönüştürdüğümüz model matrisidir.

İlk olarak, her bir küp için dünya uzayındaki konumunu belirten bir dönüşüm vektörü tanımlayalım. Birglm::vec3 dizisinde 10 küp konumu tanımlayacağız:

glm::vec3 cubePositions[] = {
    glm::vec3( 0.0f,  0.0f,  0.0f), 
    glm::vec3( 2.0f,  5.0f, -15.0f), 
    glm::vec3(-1.5f, -2.2f, -2.5f),  
    glm::vec3(-3.8f, -2.0f, -12.3f),  
    glm::vec3( 2.4f, -0.4f, -3.5f),  
    glm::vec3(-1.7f,  3.0f, -7.5f),  
    glm::vec3( 1.3f, -2.0f, -2.5f),  
    glm::vec3( 1.5f,  2.0f, -2.5f), 
    glm::vec3( 1.5f,  0.2f, -1.5f), 
    glm::vec3(-1.3f,  1.0f, -1.5f)  
};

Şimdi, sahneleme döngüsü içinde glDrawArrays'i 10 kez çağırmak istiyoruz, ancak bu kez çizim çağrısını göndermeden önce köşe nokta gölgelendiricisine farklı bir model matrisi gönderiyoruz. Sahneleme döngüsünde, nesnemizi her seferinde farklı bir model matrisi ile 10 kez işleyen küçük bir döngü oluşturacağız. Ayrıca, her bir konteynere farklı küçük birer dönme eklediğimizi unutmayın.

glBindVertexArray(VAO);
for(unsigned int i = 0; i < 10; i++)
{
    glm::mat4 model = glm::mat4(1.0f);
    model = glm::translate(model, cubePositions[i]);
    float angle = 20.0f * i; 
    model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
    ourShader.setMat4("model", model);

    glDrawArrays(GL_TRIANGLES, 0, 36);
}

Bu kod parçası, her yeni küp çiziminde model matrisini güncelleyecek ve bu toplamda 10 kez gerçekleştirecek. Şu anda tuhaf şekilde döndürülmüş 10 adet küple dolu bir dünyaya bakıyoruz:

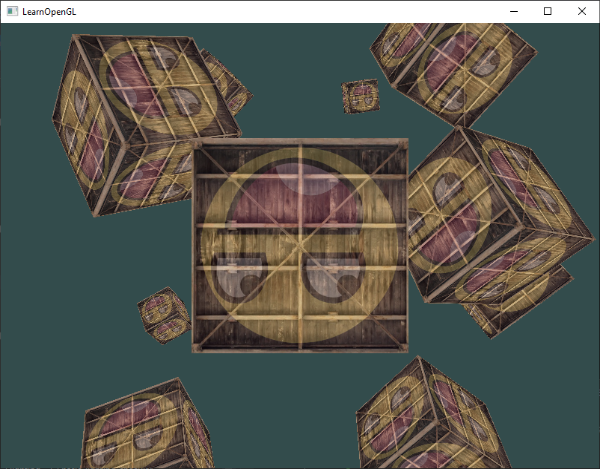
Mükemmel! Konteynerimizin hemfikir olduğu bazı arkadaşlar bulduğu anlaşılıyor 😊 Takılırsanız, kodunuzu kaynak kodla karşılaştırabilirsiniz.

Alıştırmalar

GLM' in projectionfonksiyonunun FoVve aspect-ratioparametrelerini değiştirmeyi deneyin. Bunların izdüşüm frustumunu nasıl etkilediğini anlayabilirsiniz.
Birkaç yöne öteleyerek görünüm matrisi ile oynayın ve sahnenin nasıl değiştiğini görün. Görünüm matrisini bir kamera nesnesi olarak düşünün.
Diğer konteynerleri yalnızca model matrisini kullanarak sabit tutarken, her bir üçüncü konteyneri (birinci konteyner dahil) zaman içinde döndürmeye çalışın: çözüm

Orijinal Kaynak: Coordinate Systems

Çeviri: Nezihe Sözen

PreviousDönüşümler NextKamera

Last updated 3 years ago