Derinlik testi

Koordinat sistemleri bölümünde, 3B bir konteyner oluşturduk ve öndeki üçgenlerin diğer üçgenlerin arkasında olması gerekirken görüntülenmesini önlemek için bir $\color{green}derinlik\ arabelleği$ kullandık. Bu bölümde, derinlik arabelleğinin (veya z-arabelleği) sakladığı $\color{green}derinlik\ değerleri$ ve bir parçanın önde olup olmadığını nasıl belirlediğini biraz daha ayrıntılı olarak inceleyeceğiz.

Derinlik arabelleği, tıpkı $\color{green}renk\ arabelleği$ renk arabelleği gibi (tüm parça renklerini depolayan: görsel çıktı), parça başına bilgi depolayan ve renk arabelleğiyle aynı genişlik ve yüksekliğe sahip bir arabellektir. Derinlik tamponu, pencereleme sistemi tarafından otomatik olarak oluşturulur ve derinlik değerlerini 16, 24 ya da32 bit float değerler olarak depolar. Çoğu sistemde 24bit hassasiyetli bir derinlik tamponu görürsünüz.

Derinlik testi etkinleştirildiğinde OpenGL, bir parçanın derinlik değerini derinlik arabelleğinin içeriğine göre test eder. OpenGL bir derinlik testi gerçekleştirir ve bu test başarılı olursa, parça oluşturulur ve derinlik tamponu yeni derinlik değeriyle güncellenir. Derinlik testi başarısız olursa, parça atılır.

Parça gölgelendiricisi çalıştırıldıktan sonra (ve bir sonraki bölümde alacağımız şablon testinden sonra) ekran alanında derinlik testi yapılır. Ekran uzayı koordinatları, OpenGL' in $\color{red}glViewport$ işlevi tarafından tanımlanan görüş alanıyla doğrudan ilişkilidir ve GLSL' in parça gölgelendiricisindeki yerleşik $\color{blue}glFragCoord$ değişkeni aracılığıyla erişilebilir. $\color{blue}glFragCoord$' un x ve y bileşenleri, parçanın ekran uzayı koordinatlarını temsil eder ((0,0) sol alt köşedir). $\color{blue}glFragCoord$ değişkeni ayrıca parçanın derinlik değerini içeren bir z bileşeni içerir. Bu z- değeri, derinlik arabelleğinin içeriğiyle karşılaştırılan değerdir.

Günümüzde çoğu GPU, $\color{green} erken\ derinlik\ testi$ adı verilen bir donanım özelliğini desteklemektedir. Erken derinlik testi, derinlik testinin parça gölgelendiricisi koşulmadan önce çalışmasına izin verir. Bir parçanın görünemeyeceği (diğer nesnelerin arkasında olduğu) anlaşıldığı zaman, parçayı erkenden terk edebiliriz.

Parça gölgelendiricileri oldukça maliyetlidir, bu nedenle onları çalıştırmaktan mümkü olduğunca kaçınmamız gerekir. Erken derinlik testi için parça gölgelendiricisindeki bir kısıtlama da, parçanın derinlik değerine yazmamamız gerektiğidir. Bir parça gölgelendiricisi derinlik değerine yazacaksa, erken derinlik testi yapmak imkansızdır; yani OpenGL, derinlik değerini önceden bulamayacaktır.

Derinlik testi varsayılan olarak devre dışıdır, bu nedenle derinlik testini etkinleştirmek için GL_DEPTH_TEST seçeneğiyle etkinleştirmemiz gerekir:

glEnable(GL_DEPTH_TEST);  

Etkinleştirildikten sonra OpenGL, derinlik testini geçen parçaların z-değerlerini otomatik olarak derinlik arabelleğinde saklar ve derinlik testini geçemezlerse parçaları atar. Derinlik testini etkinleştirdiyseniz, GL_DEPTH_BUFFER_BIT kullanarak her çerçeveden önce derinlik tamponunu da temizlemelisiniz; aksi takdirde, son karedeki derinlik değerlerine bağlı kalırsınız:

glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);  

Tüm parçalar üzerinde derinlik testi yapmak ve bunları uygun şekilde atmak, ancak derinlik tamponunu güncellememek isteyeceğiniz bazı senaryolar olabilir. Temel olarak, $\color{green} salt\ okunur$ bir derinlik arabelleği kullanıyoruz. OpenGL, derinlik maskesini GL_FALSE olarak ayarlayarak derinlik arabelleğine yazmayı devre dışı bırakmamızı sağlar:

glDepthMask(GL_FALSE);  

Bunun yalnızca derinlik testi etkinleştirildiğinde etkili olduğunu unutmayın.

Derinlik test işlevi

OpenGL, derinlik testi için kullandığı karşılaştırma operatörlerini değiştirmemize olanak tanır. Bu, OpenGL'in parçaları ne zaman geçirmesi veya atması gerektiğini ve derinlik arabelleğini ne zaman güncelleyeceğimizi kontrol edebilmemizi sağlar. Karşılaştırma operatörünü (veya derinlik işlevini) $\color{red}glDepthFunc$ 'u çağırarak ayarlayabiliriz:

glDepthFunc(GL_LESS); 

İşlev, aşağıdaki tabloda listelenen birkaç karşılaştırma operatörünü kabul eder:

İşlev	Açıklama
GL_ALWAYS	Derinlik testi her zaman geçer.
GL_NEVER	Derinlik testi asla geçmez.
GL_LESS	Parçanın derinlik değeri depolanan derinlik değerinden küçükse geçer.
GL_EQUAL	Parçanın derinlik değeri, depolanan derinlik değerine eşitse geçer.
GL_LEQUAL	Parçanın derinlik değeri depolanan derinlik değerine eşit veya daha az ise geçer.
GL_GREATER	Parçanın derinlik değeri depolanan derinlik değerinden büyükse geçer.
GL_NOTEQUAL	Parçanın derinlik değeri, depolanan derinlik değerine eşit değilse geçer.
GL_GEQUAL	Parçanın derinlik değeri depolanan derinlik değerine eşit veya daha büyük ise geçer.

Varsayılan olarak, derinlik değeri geçerli derinlik arabelleğinin değerinden daha yüksek veya ona eşit olan tüm parçaları atan GL_LESS derinlik işlevi kullanılır.

Derinlik fonksiyonunu değiştirmenin görsel çıktı üzerindeki etkisini gösterelim. Aydınlatmasız dokulu bir zeminde oturan iki dokulu küp ile temel bir sahneyi görüntüleyen yeni bir kod kurulumu kullanacağız. Kaynak kodunu burada bulabilirsiniz.

Kaynak kodda derinlik işlevini GL_ALWAYS olarak değiştirdik:

glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_ALWAYS); 

Bu, derinlik testini etkinleştirmezsek elde edeceğimiz aynı davranışı benzetimler. Derinlik testini her zaman geçer, böylece en son çizilen parçalar, ön tarafta olmaları gerekse bile daha önce çizilen parçaların önünde işlenir. Zemin düzlemini en son çizdiğimiz için, uçağın parçaları, konteynerin önceden yazılmış parçalarının her birinin üzerine yazıyor:

Hepsini GL_LESS olarak ayarlamak bize alışık olduğumuz sahne türünü verecektir:

Derinlik değeri hassasiyeti

Derinlik arabelleği, 0.0 ile 1.0 arasında derinlik değerleri içerir ve içeriğini, görüldüğü gibi sahnedeki tüm nesnelerin z-değerleri ile karşılaştırır. Görünüm alanındaki bu z-değerleri, projeksiyon-frustum' un yakın ve uzak düzlemi arasındaki herhangi bir değer olabilir. Bu nedenle, bu görüş alanı z- değerlerini[0,1]aralığına dönüştürmek için bir yola ihtiyacımız var ve bu yol da onları doğrusal olarak dönüştürmektir. Aşağıdaki (doğrusal) denklem, z- değerini 0.0 ile 1.0 arasında bir derinlik değerine dönüştürür:

\begin{equation} F_{depth} = \frac{z - near}{far - near} \end{equation}

Burada yakın ve uzak, görünür frustumu ayarlamak için projeksiyon matrisine sağladığımız yakın ve uzak değerlerdir (bakınız Koordinat Sistemleri). Denklem, kesiklik içinde bir derinlik değeri olan z' yi alır ve bunu[0,1]aralığına dönüştürür. z-değeri ile ona karşılık gelen derinlik değeri arasındaki ilişki aşağıdaki grafikte gösterilmektedir:

Tüm denklemlerin, nesne yakın olduğunda 0.0'a yakın bir derinlik değeri ve nesne uzak düzleme yakın olduğunda 1.0'a yakın bir derinlik değeri verdiğine dikkat edin.

In practice however, alinear depth buffer like this is almost never used. Because of projection properties a non-linear depth equation is used that is proportional to 1/z. The result is that we get enormous precision when z is small and much less precision when z is far away.

Since the non-linear function is proportional to 1/z, z-values between 1.0 and 2.0 would result in depth values between 1.0 and 0.5 which is half of the [0,1] range, giving us enormous precision at small z-values. Z-values between 50.0 and 100.0 would account for only 2% of the [0,1] range. Such an equation, that also takes near and far distances into account, is given below:

$$\begin{equation} F_{depth} = \frac{1/z - 1/near}{1/far - 1/near} \end{equation}$$

Don't worry if you don't know exactly what is going on with this equation. The important thing to remember is that the values in the depth buffer are not linear in clip-space (they are linear in view-space before the projection matrix is applied). A value of 0.5 in the depth buffer does not mean the pixel's z-value is halfway in the frustum; the z-value of the vertex is actually quite close to the near plane! You can see the non-linear relation between the z-value and the resulting depth buffer's value in the following graph:

Graph of depth values in OpenGL as a non-linear function

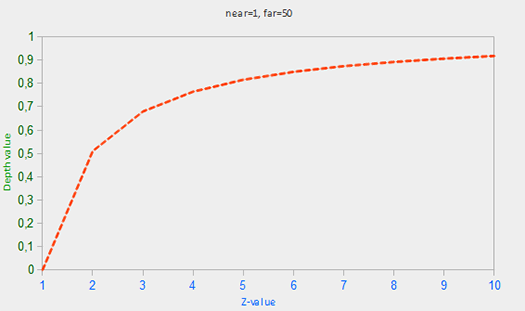
As you can see, the depth values are greatly determined by the small z-values giving us large depth precision to the objects close by. The equation to transform z-values (from the viewer's perspective) is embedded within the projection matrix so when we transform vertex coordinates from view to clip, and then to screen-space the non-linear equation is applied.

The effect of this non-linear equation quickly becomes apparent when we try to visualize the depth buffer.

Visualizing the depth buffer

We know that the z-value of the built-in gl_FragCoord vector in the fragment shader contains the depth value of that particular fragment. If we were to output this depth value of the fragment as a color we could display the depth values of all the fragments in the scene:

void main()
{             
    FragColor = vec4(vec3(gl_FragCoord.z), 1.0);
}  

If you'd then run the program you'll probably notice that everything is white, making it look like all of our depth values are the maximum depth value of 1.0. So why aren't any of the depth values closer to 0.0 and thus darker?

In the previous section we described that depth values in screen space are non-linear e.g. they have a very high precision for small z-values and a low precision for large z-values. The depth value of the fragment increases rapidly over distance so almost all the vertices have values close to 1.0. If we were to carefully move really close to an object you may eventually see the colors getting darker, their z-values becoming smaller:

Depth buffer visualized in OpenGL and GLSL

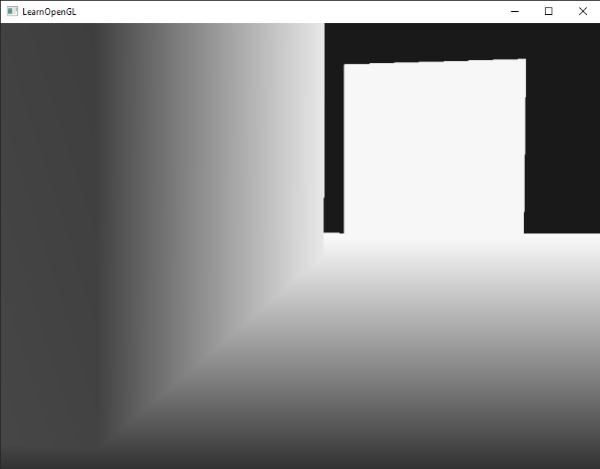
This clearly shows the non-linearity of the depth value. Objects close by have a much larger effect on the depth value than objects far away. Only moving a few inches can result in the colors going from dark to completely white.

We can however, transform the non-linear depth values of the fragment back to its linear sibling. To achieve this we basically need to reverse the process of projection for the depth values alone. This means we have to first re-transform the depth values from the range [0,1] to normalized device coordinates in the range [-1,1]. Then we want to reverse the non-linear equation (equation 2) as done in the projection matrix and apply this inversed equation to the resulting depth value. The result is then a linear depth value.

First we transform the depth value to NDC which is not too difficult:

float ndc = depth * 2.0 - 1.0; 

We then take the resulting ndc value and apply the inverse transformation to retrieve its linear depth value:

float linearDepth = (2.0 * near * far) / (far + near - ndc * (far - near));	

This equation is derived from the projection matrix for non-linearizing the depth values, returning depth values between near and far. This math-heavy article explains the projection matrix in enormous detail for the interested reader; it also shows where the equations come from.

The complete fragment shader that transforms the non-linear depth in screen-space to a linear depth value is then as follows:

#version 330 core
out vec4 FragColor;

float near = 0.1; 
float far  = 100.0; 
  
float LinearizeDepth(float depth) 
{
    float z = depth * 2.0 - 1.0; // back to NDC 
    return (2.0 * near * far) / (far + near - z * (far - near));	
}

void main()
{             
    float depth = LinearizeDepth(gl_FragCoord.z) / far; // divide by far for demonstration
    FragColor = vec4(vec3(depth), 1.0);
}

Because the linearized depth values range from near to far most of its values will be above 1.0 and displayed as completely white. By dividing the linear depth value by far in themain function we convert the linear depth value to the range [0, 1]. This way we can gradually see the scene become brighter the closer the fragments are to the projection frustum's far plane, which works better for visualization purposes.

If we'd now run the application we get depth values that are linear over distance. Try moving around the scene to see the depth values change in a linear fashion.

Depth buffer visualized in OpenGL and GLSL as linear values

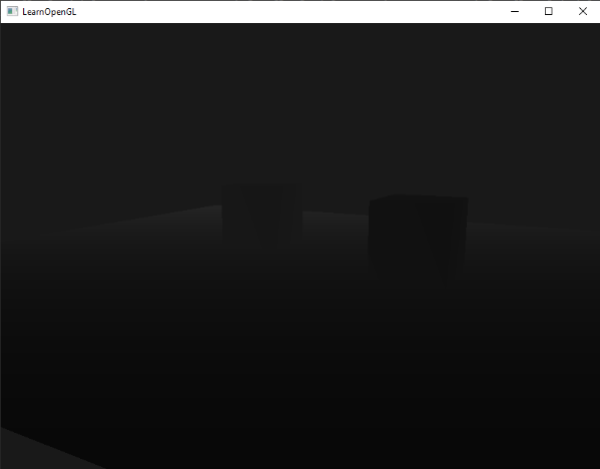
The colors are mostly black because the depth values range linearly from the near plane (0.1) to the far plane (100) which is still quite far away from us. The result is that we're relatively close to the near plane and therefore get lower (darker) depth values.

Z-fighting

A common visual artifact may occur when two planes or triangles are so closely aligned to each other that the depth buffer does not have enough precision to figure out which one of the two shapes is in front of the other. The result is that the two shapes continually seem to switch order which causes weird glitchy patterns. This is calledz-fighting, because it looks like the shapes are fighting over who gets on top.

In the scene we've been using so far there are a few spots where z-fighting can be noticed. The containers were placed at the exact height of the floor which means the bottom plane of the container is coplanar with the floor plane. The depth values of both planes are then the same so the resulting depth test has no way of figuring out which is the right one.

If you move the camera inside one of the containers the effects are clearly visible, the bottom part of the container is constantly switching between the container's plane and the floor's plane in a zigzag pattern:

Demonstration of Z-fighting in OpenGL

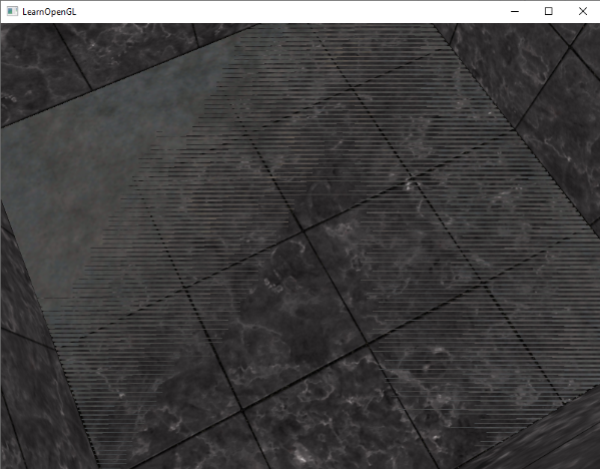
Z-fighting is a common problem with depth buffers and it's generally more noticeable when objects are further away (because the depth buffer has less precision at larger z-values). Z-fighting can't be completely prevented, but there are a few tricks that will help to mitigate or completely prevent z-fighting in your scene.

Prevent z-fighting

The first and most important trick is never place objects too close to each other in a way that some of their triangles closely overlap. By creating a small offset between two objects you can completely remove z-fighting between the two objects. In the case of the containers and the plane we could've easily moved the containers slightly upwards in the positive y direction. The small change of the container's positions would probably not be noticeable at all and would completely reduce the z-fighting. However, this requires manual intervention of each of the objects and thorough testing to make sure no objects in a scene produce z-fighting.

A second trick is to set the near plane as far as possible. In one of the previous sections we've discussed that precision is extremely large when close to the near plane so if we move the near plane away from the viewer, we'll have significantly greater precision over the entire frustum range. However, setting the near plane too far could cause clipping of near objects so it is usually a matter of tweaking and experimentation to figure out the best near distance for your scene.

Another great trick at the cost of some performance is to use a higher precision depth buffer. Most depth buffers have a precision of 24 bits, but most GPUs nowadays support 32 bit depth buffers, increasing the precision by a significant amount. So at the cost of some performance you'll get much more precision with depth testing, reducing z-fighting.

The 3 techniques we've discussed are the most common and easy-to-implement anti z-fighting techniques. There are some other techniques out there that require a lot more work and still won't completely disable z-fighting. Z-fighting is a common issue, but if you use the proper combination of the listed techniques you probably won't need to deal with z-fighting that much.

Orijinal Kaynak: Depth testing

Çeviri: Nezihe Sözen